-
核物质状态方程即表征核物质能量(或压强)与密度(或化学势)以及温度、同位旋不对称度等量的关系,是核物质性质的最基本和最重要的表述之一。它的信息对原子核结构和反应、中子星等的研究具有十分重要的意义[1-4]。由于重离子碰撞过程能产生高温高密的核物质,因此利用重离子碰撞去研究核物质状态方程是目前最常用的手段之一。目前人们对核物质状态方程的信息已经有一些了解,由于重离子碰撞过程持续时间十分短暂,实验上不能直接测量其性质,通常需要结合输运模型来模拟重离子碰撞的过程从而抽取核物质状态方程的信息[5-8]。随着国内外许多大科学装置,如FAIR,FRIB,HIAF,NICA等相继建成和投入使用,为核物质状态方程的研究提供了新机遇[9-12]。
如何更好地分析和利用“大数据”一直以来是人们关注的热点之一。从20世纪80年代开始,物理学家们就使用支持向量机(SVM)、贝叶斯概率分析(BP)和逻辑回归(LR)等方法去研究粒子物理、凝聚态物理、生物物理、天文和量子计算等领域内相应的问题[13-18]。随着计算框架和设备的不断革新,计算速度与分析效率显著提升,机器学习(ML)和深度学习(DL)得到了更多的关注与更好的发展[19-21]。在这之中,尤其是根据模拟大脑运作方式提出的神经元网络框架[22],例如卷积神经元网络(CNN,Convolutional Neural Network)、循环神经网络(RNN,Recurrent Neural Network)和生成对抗网络(GAN,Generative Adversarial Networks)等方法被成功地用于多个科学领域的研究。例如,华中师范大学的庞龙刚教授等利用深度学习中的CNN方法来识别强相互作用物质的相变模式[23];北京大学的裴俊琛教授等利用贝叶斯神经元网络(BNN,Bayesian Neural Networks)方法预测裂变产额[24]。在之前的研究工作中[25],我们使用基于决策树的LightGBM与CNN这两种算法对碰撞参数进行了重构。其重构精度
$ \Delta b $ (预测值与真实值之间的平均偏差)能小于0.1 fm。这说明通过提取末态质子的快度和动量分布,能够很好地判定初态的碰撞参数。此外,我们还对入射能量的依赖以及机器学习模型的泛化能力进行了详细的研究,其结果说明在一定入射能量的范围内,机器学习重构碰撞参数的结果是合理的。这些研究表明,利用深度学习方法研究和处理数据,能够挖掘数据背后的有效信息,为研究具体物理问题提供新思路。通过重离子反应实验,我们可以获得大量末态粒子在动量空间中的分布数据,但是从这些数据中直接观察出其规律性,抽取核物质信息是十分困难的事情。通常情况下,可以通过构建一些可观测物理量(如,集体流、核阻止本领、粒子产额等),核物质状态方程会影响这些观测量的值,从而帮助我们推断出核物质的性质。而深度学习方法,直接对不同状态方程给出的动量空间的分布数据进行分析和“学习”,会自动寻找数据点之间的关联、差异以及背后隐含的信息,从而具有识别核物质状态方程的能力。一般而言,如果传统观测量上能体现核状态方程的影响,深度学习方法也可以区分状态方程的影响;如果传统的观测量不能体现出状态方程的影响,深度学习技术也可能通过自主构建和寻找的特征量(这个量不一定会有明确的物理意义)来实现区分状态方程影响的效果。此外,在深度学习的过程中,还能给出数据分布区域中对结果影响最大的区域,能为理论和实验提供一个可以关注的窗口。深度学习技术用于分析物理问题时的可解释性仍然需要进一步研究[26-27]。
本文使用极端相对论量子分子动力学(UrQMD)输运模型模拟重离子碰撞过程,产生大量末态粒子的状态数据(如快度和动量分布等)。然后借助CNN和分布式梯度提升算法(LightGBM)对这些数据进行学习,探索数据背后隐含信息,使其具有从末态粒子数据分辨核物质状态方程软硬的能力。并且结合两种可解释性方法,对这些状态数据分布进行探测从而获得较为敏感的分布区域,为开展更高精度的实验提供窗口。
文章由以下几个部分组成:首先,在第2节对UrQMD模型进行简单介绍并且对不同核物质状态方程模拟的末态质子快度和横动量分布进行讨论。然后,在第3节介绍本文所使用的CNN和LightGBM方法。接下来,在第4节讨论了使用两种方法区分核物质状态方程软硬的结果。最后,在第5节对文章进行了总结与展望。
-
UrQMD模型包括初始化、势修正、碰撞项等几个部分。随着模型的不断改进,现在的版本在势修正部分引入了Skyrme势能密度泛函,在碰撞项部分对两体碰撞截面考虑了介质修正,以及在输运模型的后期碎片重构模式中采用了同位旋依赖性的处理[28-29]。经过这些改进后,该模型能够很好地解释中能区重离子碰撞中的大量实验数据[30]。
在UrQMD模型中,粒子被看做是有一定宽度的高斯波包,其坐标
$ {\boldsymbol r}_{i} $ 和动量$ {\boldsymbol p}_{i} $ 随时间的演化由哈密顿运动方程来描述:$$ {\boldsymbol{r}}_{i} = \frac {\partial H} {\partial {\boldsymbol{p}}_{i}},\; \; {\boldsymbol{p}}_{i} = -\frac {\partial H} {\partial {\boldsymbol{r}}_{i}}, $$ (1) 其中哈密顿量
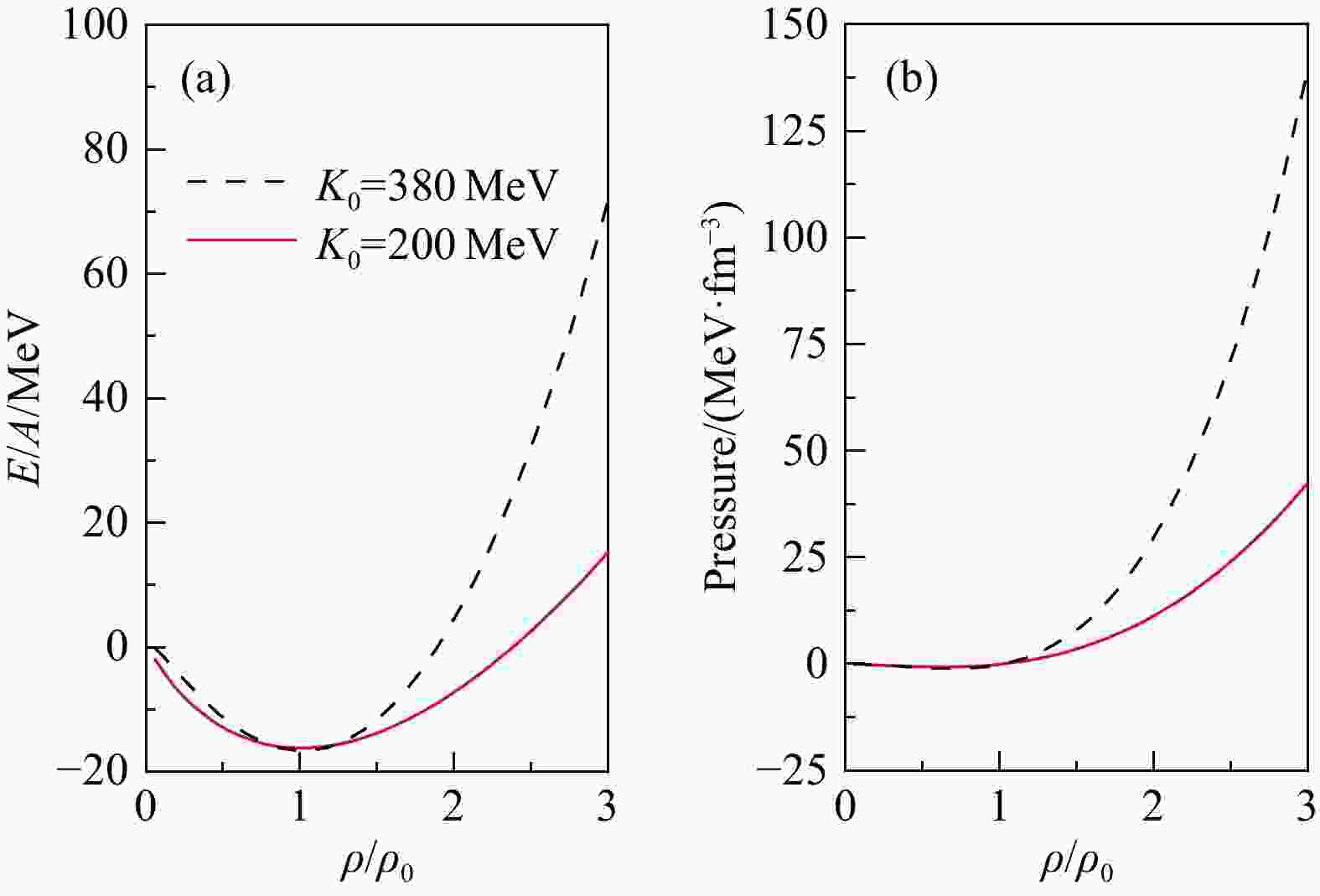
$ H $ 由动能和相互作用势能组成。势能可以采用Skyrme势能密度泛函形式来描述[30]。除此之外,还考虑了动量相关项和库仑势[31]。通过选取不同的势能参数就可以给出不同的状态方程[31]。本文所采用的参数有两组,一组给出的核物质不可压缩系数$ K_0 = $ $ 9\rho^2\left(\frac{\partial ^2E/A} {\partial \rho^2}\right)\big|_{\rho = \rho_{0}} = 9\left(\frac{\partial {P}} {\partial \rho}\right)\big|_{\rho = \rho_{0}} = 200 $ MeV,称为“软”的状态方程(简写:SM);另一组为$ K_0 = 380 $ MeV,称为“硬”的状态方程(简写:HM)。图1显示的是根据这两组参数计算出的每核子能量(a)和压强(b)随约化密度(其中$ \rho_{0} $ 为核物质饱和密度)的变化情况。该图表明,在高于饱和密度$ (\rho/\rho_{0} > 1) $ 的区域,这两组状态方程给出的结果有明显差异。本文选取了入射能量在每核子0.4 GeV的Au与Au碰撞来研究状态方程软硬对重离子碰撞过程的影响。为进一步探究不同碰撞参数下的情况,选取了
$ b = 0 $ 和5 fm这两种情况进行模拟。对末态质子数的横动量$ p_{\rm t} = $ $ \sqrt{p_x^2+p_y^2} $ 和约化快度$ y_{0} = y_z/y_{\rm pro} $ (其中$ y_{z} = \frac{1}{2}\ln[\frac{E+p_{z}}{E-p_{z}}] $ 是粒子在质心系下的快度,$ y_{\rm pro} $ 为入射弹核的快度)分布进行分析。选取的范围为:$ 0\leqslant p_{\rm t}\leqslant 1 $ GeV/c和$ -2\leqslant $ $ y_{0} \leqslant2 $ 。在本文采用的入射能量下,上述范围能够包含99%以上的质子数目。如果将$ p_{\rm t} $ 划分为20个区间、$ y_{0} $ 划分为40个区间,这样就可以获得一张“像素”为$ 20\times $ $ 40 $ 的图片,并将这张图片的数据作为神经网络的输入量。经测试发现,当像素的取值在一个合理的范围内时,不会对结果的准确度造成太大的影响。一方面,如果像素选取的太小,即每个像素点对应的$ y_{0} $ 和$ p_{\rm t} $ 的范围较大,将很容易丢失质子数随$ y_{0} $ 和$ p_{\rm t} $ 分布的一些细节信息;另一方面,如果像素选取的太大,每个像素点对应的$ y_{0} $ 和$ p_{\rm t} $ 的范围就很小,每次碰撞对应到某个像素点的质子数目就会有较大差异,即有较大涨落。这种涨落容易掩盖由不同状态方程所引起的质子数分布差异。图2显示了随机挑选的五个事件的末态质子(用不同颜色的小球表示)的
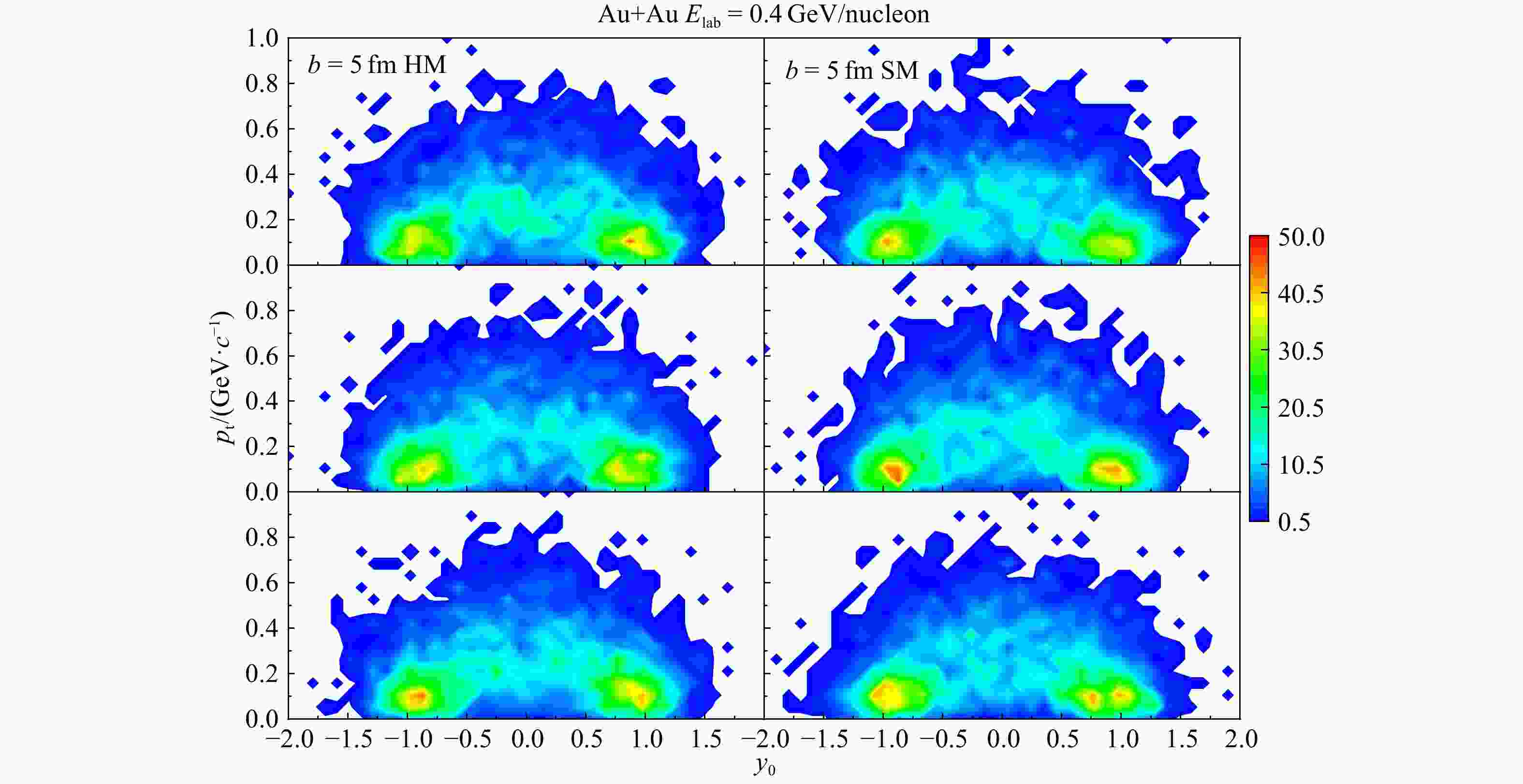
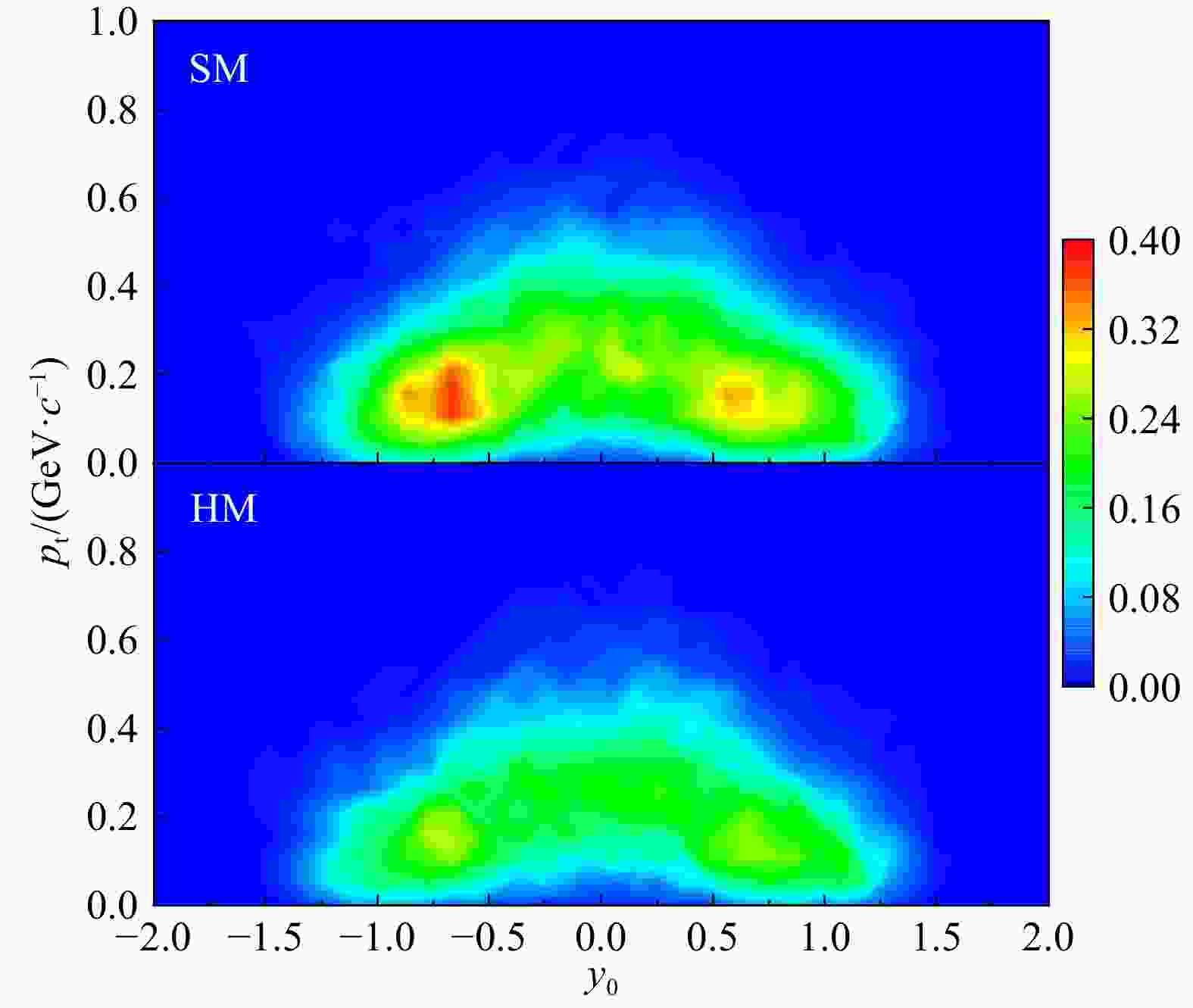
$ y_{0} $ -$ p_{\rm t} $ 分布情况。因为输运过程中有很多随机的核子-核子碰撞以及初始化时原子核涨落的存在,不同事件给出的末态分布都很不相同。对比不同状态方程给出的结果,肉眼很难发现其本质区别。其次,碰撞参数为0 fm的质子分布主要集中在中心快度区域,而碰撞参数为5 fm时其分布主要集中在$ y_{0} = \pm1 $ 处。这是因为$ b = 0 $ fm 时,大多数粒子的纵向运动被阻止,所以粒子的快度集中在中心快度附近,而$ b = $ $ 5 $ fm时,大多数粒子经历的碰撞次数很少,更容易保持最初的快度值($ \pm1 $ )。通常情况下,模拟上万次事件后,求某些量的平均值,就可以明显减弱随机涨落所带来对结果的影响,显现出不同状态方程的影响。在本次研究中,首先试图从单个或者几十个事件观测量中观察不同状态方程的影响。下面,就随机挑选20个事件叠加成一个样本,来进一步观察末态质子分布的情况。图3是碰撞参数为5 fm时,20个事件叠加后得到的质子的
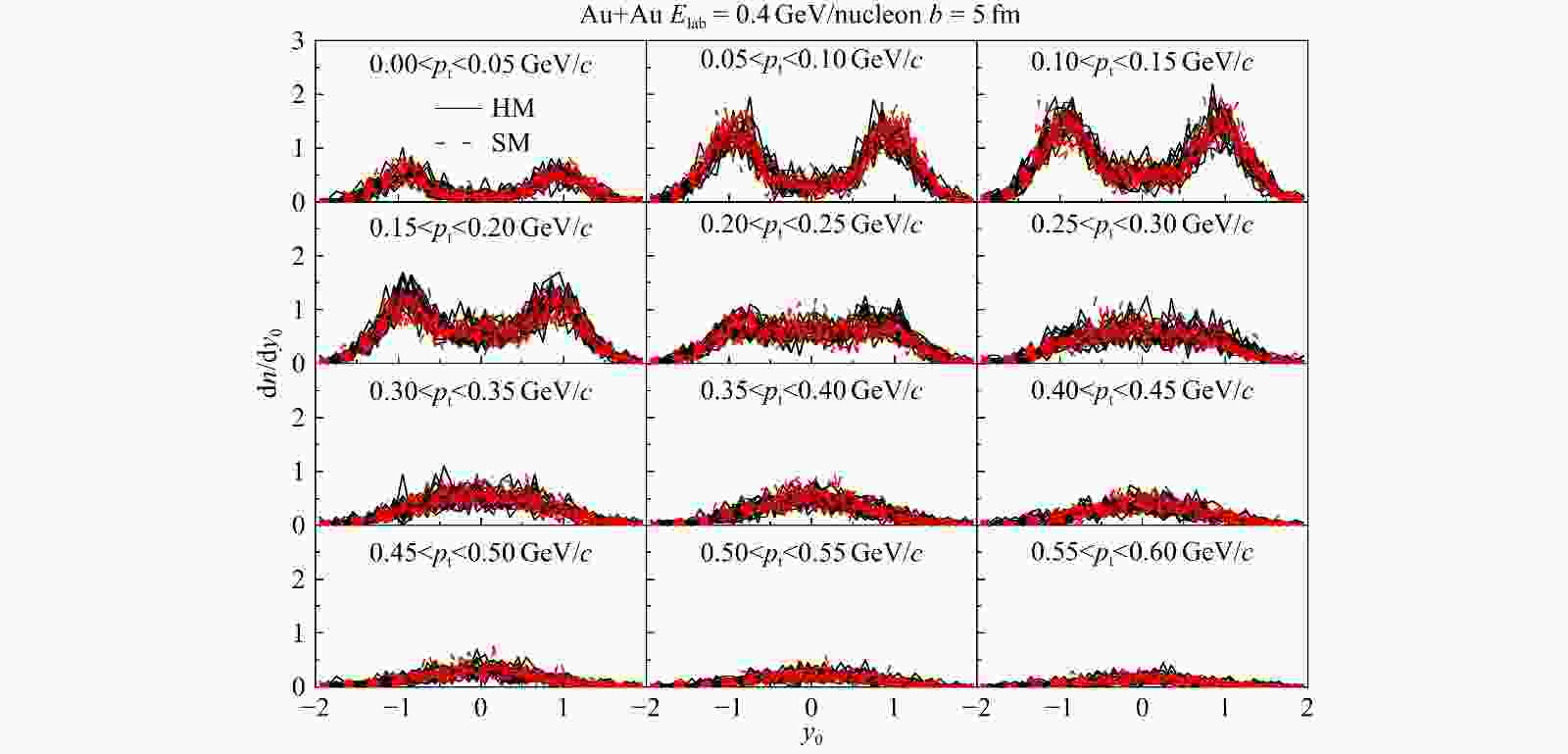
$ y_{0} $ -$ p_{\rm t} $ 分布。经过叠加后,尽管不同样本之间的涨落有所减弱,但是不同状态方程给出的结果差异仍然不易观察到。在图4中进一步显示了在不同横动量区间质子的快度分布。每个图中显示了20个样本的结果。虽然,很明显在不同横动量区其产额的快度分布各不相同,但是,从每一个样本(均是20个事件的叠加)不同横动量区的结果看,仍然很难观察到状态方程的影响差异。通过对图2~4的观察,可以发现,不管是单事件还是20个事件叠加后得到的样本,状态方程对其末态质子分布的影响差异都很难区分。 -
CNN主要包括输入层(input layer),卷积层(convolutional layer),池化层(pooling layer),全连接层(fully connected layer)和输出层(output layer)等几个部分。输入层输入类型可以是数据、文本或者图片。卷积层是CNN最核心的部分之一,由多个卷积核组成,每个卷积核都有相对应的权重和偏差量,对输入层的输入量进行特征提取。卷积过程的数学表达式为
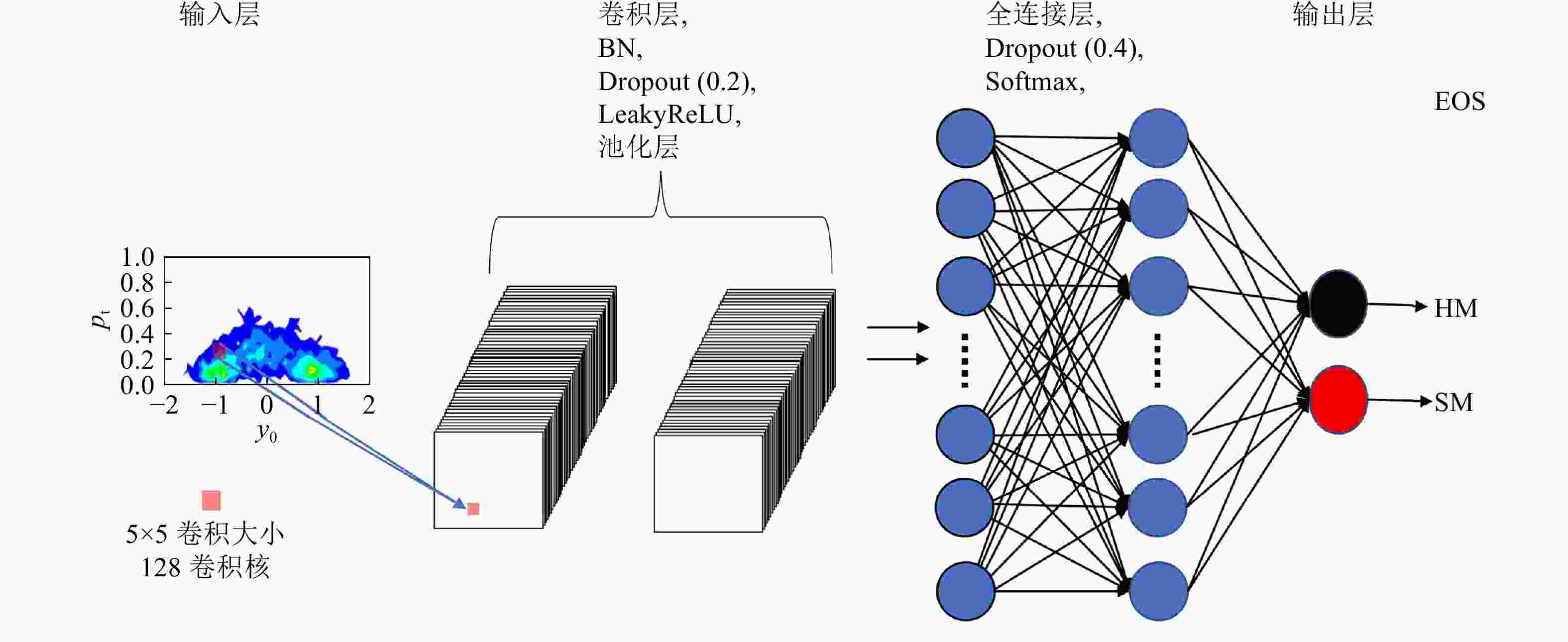
$ s_{i,j} = $ $ \sum_{k = 1}^n (X_{k}\bigotimes W_{k})_{i,j} + b_{i,j} $ ,其中n对应卷积层卷积核的数量,即“通道(channel)”。$ X_{k} $ 和$ W_{k} $ 分别代表第k个输入矩阵和卷积核第k个卷积核矩阵。卷积核的大小也被称为“感受视野”,会影响参数的数量,以及每次训练的时长和识别的准确度等,$ W_{k} $ 又被称为权重矩阵(Weight)。$ b_{i,j} $ 为偏差量(bias),$ s_{i,j} $ 为输出的对应元素值。池化层同样也可以选择卷积的方式,对数据进行再一次特征选择和过滤。经过卷积层和池化层以后,全连接层将卷积层或者池化层中具有类别区别的特征综合起来。最后的输出层为我们的输出结果,对于分类问题,输出结果一般为预测的类别。为了优化训练的结果,解决在训练过程中出现的梯度弥散、数据分布不均衡、过拟合和欠拟合等问题,在层与层之间通常还可以加入批归一化(BN,batch normalization)、随机失活(Dropout)、激活函数(activation)以及正则化(regularization)等过程[32-33]。本文研究的问题属于二分类问题,因此在数据输入之前用(0,1)方式标记(HM,SM)两种状态方程下UrQMD模型的计算结果,以便于对不同类别的数据进行识别,保证输出的结果非0即1。图5显示的是我们目前所使用的模型框架及其参数设置。我们选择了两个卷积层,每个卷积层中的卷积核数量为128,大小为
$ 5\times5 $ ,在每个卷积层后面还加入了Dropout层、BN层、激活函数LeakyReLU以及池化层。最后在全连接层和输出层之间,我们还加入了Dropout层、激活函数softmax。除此之外,本文还使用了目前机器学习最常用的数据分类算法之一:分布式梯度提升算法(LightGBM,Light Gradient Boosting Machine)[34]。LightGBM是由微软公司开发的基于梯度下降树(GBDT,Gradient Boosting Decision Tree)的一种算法。其主要包括:单边梯度采样算法(GOSS,Grandient-based One-Side Sampling)和单一特征包算法(EFB,Exclusive Feature Bundling)。GOSS主要解释了LightGBM的leaf-wise生成策略,选取具有最大增益损失的节点进行分裂,再通过max-depth来限制深度以避免过拟合。而EFB 策略则通过判断特征的相关性,对输入的特征进行分析,再将类似特征捆绑,这样能大幅地减少训练所需时间。相对于本文的输入数据,每个“像素”点就是对应特征量。LightGBM在工业数据分类上十分常见,是机器学习里面比较成熟的分类算法。本文所使用的参数基本来自于LightGBM官方给出的默认数值,更多相关介绍可以通过查阅LightGBM官方所给出的参考文献[35]。下一节就将利用这两种方法对UrQMD模拟的数据进行训练和识别。
-
在实际的训练过程中,训练集的数据量相较测试集而言会比较多,因此通常会将训练集数据划分出一部分作为验证集。这样划分目的在于能够充分利用数据的同时,还可以通过训练集和验证集的交叉验证的方式获得稳定可靠的模型。再将训练获得的模型在测试集上进行测试,测试集的准确度作为评价模型的指标之一。为了更符合真实的数据集分布,我们对此次的数据集进行了如下处理:每种状态方程我们模拟了40万次的碰撞获得80万个单事件的质子分布数据。对于单事件数据集,我们从两种状态方程中各自随机抽取20万事件(共40万)组成训练集,在训练集中又随机抽取其中的20%组成验证集进行交叉验证,从剩下的40万事件中各自抽取10万个事件(共20万个事件)组成测试集。对于20个事件叠加后的样本数据集,经过叠加处理以后从80万个单事件样本中获得了4万个样本,因此划分3万个样本组成训练集,随机抽取其中20%组成验证集,剩下的1 万个样本组成测试集。划分好数据集之后,我们将对数据集进行训练。
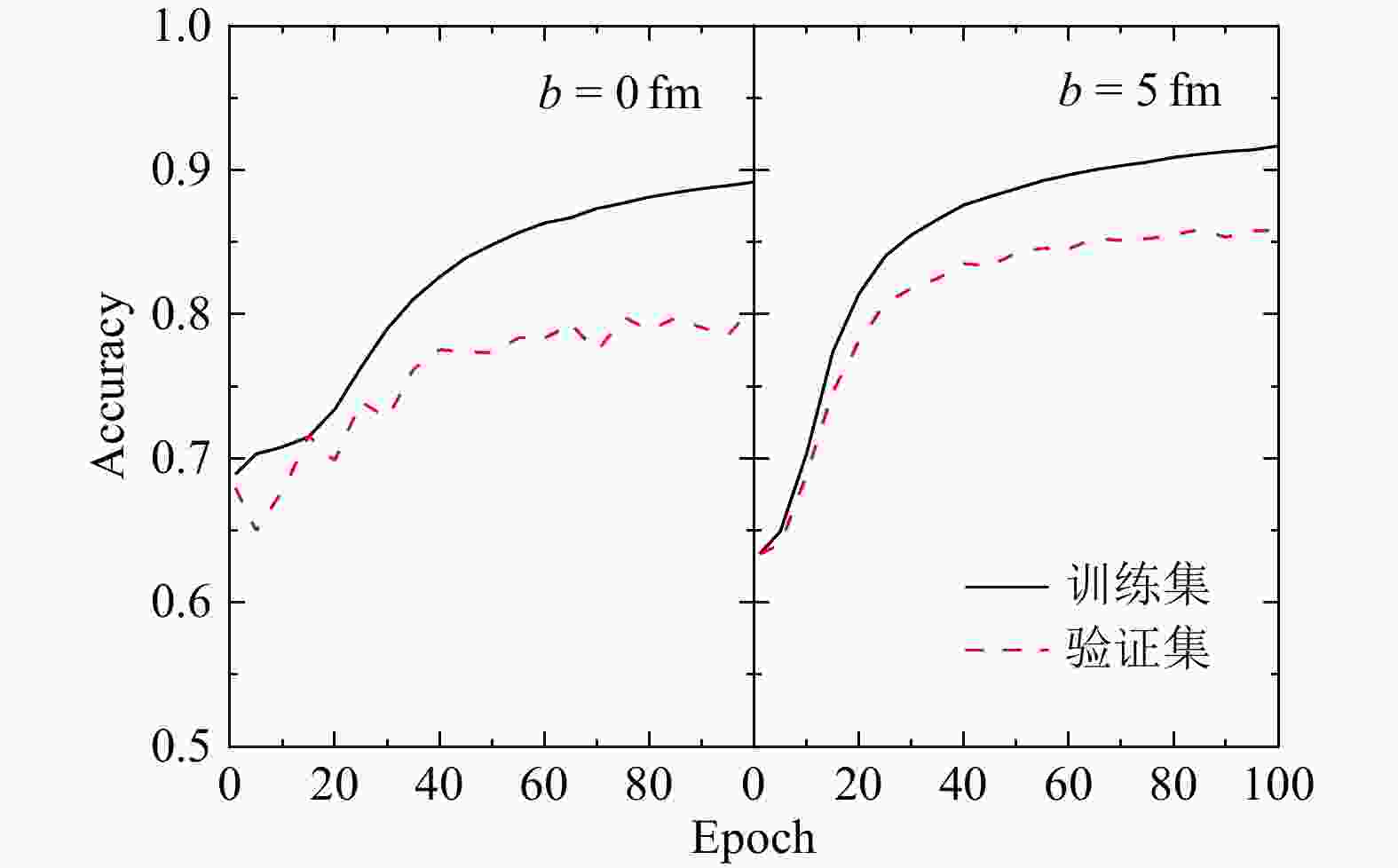
首先,我们采用单事件结果作为数据集,对碰撞参数为0和5 fm两种情况分别进行训练(见图6)。从图中可以看出,因为交叉验证的存在,使得每一次的训练都会获得对应的训练集和验证集的准确度。训练一定次数以后,训练集上的准确度超过了验证集,这种过拟合现象的出现表明训练可以停止。最后将训练好的模型在测试集进行测试,记录其准确度作为评价模型指标之一(见表1)。与此同时,我们也采用了20个事件叠加得到的样本作为数据集进行了训练。同样也将训练好的模型在测试集上进行测试并且记录(见表1)。
表 1 状态方程测试的准确度
类别 方法 $b=0$fm $b=5$fm 单事件 CNN $\approx80{\%}$ $\approx85{\%}$ LightGBM $\approx83{\%}$ $\approx85{\%}$ 20事件叠加 CNN $>96{\%}$ $>96{\%}$ LightGBM $>96{\%}$ $>96{\%}$ 在表1中,我们分别记录了CNN和LightGBM两种方法的测试结果。不难看出,不论是单事件还是叠加事件的结果,CNN与LightGBM两种方法所给出的测试结果类似。仅相对于碰撞参数为0 fm的测试结果,LightGBM方法有些许的提高。从表中我们还可以观察到碰撞参数为5 fm时,比0 fm有更高的准确度,表明在5 fm时,两种方法对于状态方程软硬的探测更加敏感一些。综上而言,对于本次的训练和测试,两种方法基本可以实现从末态质子分布来区分核物质状态方程的软硬。并且使用多事件叠加后的样本训练,可以得到更高的准确度,这是因为多事件叠加有助于减少涨落信号从而增强状态方程的影响。
此外,近些年,机器学习与深度学习模型的可解释性成为了研究的热点问题。对于可解释性的研究有助于我们更好的理解这些机器学习模型是如何从数据中提取有效的信息,做出决策的。其中深度学习中为了解决CNN可视化与可解释性问题,提出了一种预测差异分析(PDA,Prediction Different Analysis)方法[36]。PDA是通过对输入数据进行局部掩盖形成新的数据样本,用CNN训练保存下来的模型进行预测。根据预测结果的差异给出局部特征重要性,通过逐个替换就可以获得全局的重要特征图。而LightGBM中的重要特征筛选,通过对每一个特征值相关性的分析,对特征值的重要程度进行评估,也能够获得重要特征图。
图7和图8分别是我们利用这两种方法对碰撞参数
$ b = 5 $ fm时末态质子的$ y_{0} $ -$ p_{\rm t} $ 分布进行分析的结果。值得一提的是,PDA通过对不同状态方程的分析,能够给出不同状态方程各自所关注的重要特征区域。而通过LightGBM的重要特征筛选,能够给出不同状态方程共同关注的重要特征区域。从图7和图8中,我们可以看到PDA给出快度的绝对值在0.5到1、横动量在0.05到0.2 GeV/c的区域对区分状态方程最敏感。LightGBM的重要特征筛选给出的敏感区域在快度的绝对值在$ 1\pm0.5 $ 、横动量在0到0.2 GeV/c。我们发现这两者给出的重要特征区域基本一致,主要集中在弹靶快度及低横动量区域。这一点我们在图3和图4中也发现了,在该区域内,质子不仅分布较为集中而且产额也较大。这是由于在碰撞时,该区域内的质子受涨落影响较小,能够提供的初态粒子信息较为稳定。这些高敏感区域可以作为实验上重点关注的窗口,为开展相关更高要求精度的实验提供帮助。 -
用UrQMD模型模拟不同软硬状态方程时Au+Au碰撞末态质子的快度-横动量(
$y_{0}$ -$ p_{\rm t} $ )分布,并利用这些分布来区分状态方程的软硬。因为碰撞的随机性,单一事件给出的$ y_{0} $ -$ p_{\rm t} $ 分布有很大涨落,即便把20个事件的结果叠加在一起,涨落信号依然比状态方程的影响大,两种情况都无法用肉眼发现不同状态方程的差异。通过CNN和LightGBM这两种方法对末态质子的$ y_{0} $ -$ p_{\rm t} $ 分布进行学习,使其具有区分不同状态方程的能力。若利用单事件作为数据集进行训练,对碰撞参数为0 fm的数据,LightGBM方法在测试集上的准确度为83%,稍微高于CNN方法的80%。而对于碰撞参数为5 fm的测试结果,两者准确度基本相同,可以达到85%;若利用由20个事件的结果叠加后的样本作为数据集进行训练,在减弱涨落的影响后,两种方法在测试集上的准确度都可大于96%,能够达到比较好的识别效果。此外,还发现用碰撞参数为5 fm时的末态质子分布训练得到的准确度比碰撞参数为0 fm时的高。利用PDA和LightGBM的重要特征筛选还能发现$ y_{0} $ -$ p_{\rm t} $ 分布中对状态方程软硬最敏感的区域,这可以为开展有更高精度要求的相关实验提供指导。上面这些研究结果表明,深度学习的分类识别功能以及基于决策树的机器学习算法可以应用于对中能重离子碰撞的更深入研究。下一步,我们将使用深度学习对同位旋非对称核物质状态方程进行更加精细的研究,如状态方程的高阶项、对称能的斜率参数、曲率参数、核子有效质量劈裂等。此外,我们还将探索人工智能方法应用于中国HIRFL、日本RIBF、德国FAIR等重离子碰撞装置上相关实验数据的分析,从而能够为相关的理论和实验研究提供新思路和新方法。
-
摘要: 对核物质状态方程的研究将有助于人们更好地了解原子核的性质以及宇宙和星体的演化过程等基本问题。重离子碰撞能产生高温高密核物质,利用输运模型的模拟结合相关实验数据的比较是研究核物质状态方程最常用方法之一。本文利用深度学习中的卷积神经元网络(CNN)方法对不同核物质状态方程给出的末态质子横动量和快度分布进行学习,使神经元网络具有从末态粒子信息来判断核物质状态方程软硬的能力。利用预测差异分析方法(Prediction Different Analysis),可以找到横动量和快度分布中对状态方程最敏感的区域。此外,还测试了一种基于决策树的梯度提升算法(LightGBM),发现得到的准确度和CNN方法类似。Abstract: The equation of state (EOS) of nuclear matter is essential for studying the properties of nuclei and the evolution of universe and astro-objects. Heavy-ion collisions at intermediate energies permit creating nuclear matter with high density and temperature, by comparing transport model simulations with the corresponding experimental data offers one of the most important way to study the nuclear EOS. Unfortunately, different models do not always give the same results. In this work, a deep convolutional neural network (CNN) is used to identify the nuclear EOS from the spectra in transverse momentum and rapidity of protons. It is found that the network can be taken as a useful decoder to extract the nuclear EOS from the transverse momentum and rapidity distribution of protons. By using the Prediction Difference Analysis method, the most sensitive region of the transverse momentum and rapidity distribution to the nuclear EOS can be found out, which may offer an alternative strategy for experimental and theoretical studies of heavy-ion collisions. In addition, a gradient boosting framework (LightGBM) that uses tree based learning algorithms is also applied, and it is found that the accuracy obtained with the LightGBM is similar to that with CNN.
-
表 1 状态方程测试的准确度
类别 方法 $b=0$fm $b=5$fm 单事件 CNN $\approx80{\%}$ $\approx85{\%}$ LightGBM $\approx83{\%}$ $\approx85{\%}$ 20事件叠加 CNN $>96{\%}$ $>96{\%}$ LightGBM $>96{\%}$ $>96{\%}$ -
[1] LATTIMER J, PRAKASH M. Physics Reports, 2007, 442: 109. doi: 10.1016/j.physrep.2007.02.003 [2] XU J, CHECN L W, LI B A. The Astrophysical Journal, 2009, 697: 1549. doi: 10.1088/0004-637X/697/2/1549 [3] HE L Y, JIANG Y, ZHUANG P F. Phys Rev C, 2009, 79: 045205. doi: 10.1103/PhysRevC.79.045205 [4] 张丰收. 原子核物理评论, 1998, 15(04): 220. doi: 10.11804/NuclPhysRev.15.04.220 ZHANG F S. Nuclear Physics Review, 1998, 15(04): 220. (in Chinese) doi: 10.11804/NuclPhysRev.15.04.220 [5] 雍高产, 李宝安, 陈列文. 原子核物理评论, 2009, 26(2): 85. doi: 10.11804/NuclPhysRev.26.02.085 YONG G C, LI B A, CHEN L W. Nuclear Physics Review, 2009, 26(2): 85. (in Chinese) doi: 10.11804/NuclPhysRev.26.02.085 [6] 陈列文. 原子核物理评论, 2017, 34(01): 20. doi: 10.11804/NuclPhysRev.34.01.020 CHEN L W. Nuclear Physics Review, 2017, 34(01): 20. (in Chinese) doi: 10.11804/NuclPhysRev.34.01.020 [7] STOCKER H, GREINER W. Physics Reports, 1986, 137(5): 277. [8] LI B A, CHEN L W, KO C M. Physics Reports, 2008, 464: 113. doi: 10.1016/j.physrep.2008.04.005 [9] ANTONOV A N, GAIDAROV M K, IVANOV M V, et al. Nucl Instr and Meth A, 2011, 637: 60. doi: 10.1016/j.nima.2010.12.246 [10] BOLLEN G. AIP Conference Proceeding, 2010, 1224: 432. [11] YANG J C, XIA J W, XIAO G Q, et al. Nucl Instr and Meth B, 2013, 317: 263. doi: 10.1016/j.nimb.2013.08.046 [12] SISSAKIAN A N, SORIN A S. Journal of Physics G, 2009, 36: 064069. doi: 10.1088/0954-3899/36/6/064069 [13] ALWXANDER R, MIKE W, DAVID R. Nature, 2018, 560(7716): 41. doi: 10.1038/s41586-018-0361-2 [14] MICHAEL R H. Science, 2017, 355(6325): 580. doi: 10.1126/science.aam6564 [15] SCHULD M, SINAYSKIY I, PETRUCCIONE F. Contemporary Physics, 2015, 56(2): 172. doi: 10.1080/00107514.2014.964942 [16] CARRASQUILLA J, MELKO R G. Nature Physics, 2017, 13: 431. doi: 10.1038/nphys4035 [17] 刘辉, 季凯帆, 金振宇. 中国科学: 物理学 力学 天文学, 2019, 49(10): 105. LIU H, JI K F, JIN Z Y. Sci Sin-Phys Mech Astron, 2019, 49(10): 105. (in Chinese) [18] MEHTA P, BUKOV M, WANG C H, et al. Phyics Reports, 2019, 810: 1. doi: 10.1016/j.physrep.2019.03.001 [19] 汪璐. 物理, 2017, 46(9): 597. doi: 10.7693/wl20170904 WANG L. Physic, 2017, 46(9): 597. (in Chinese) doi: 10.7693/wl20170904 [20] 郜勋, 尹璋琦. 物理, 2017, 46(3): 182. GAO X, YIN Z Q. Physic, 2017, 46(3): 182. (in Chinese) [21] 程嵩, 陈靖, 王磊. 物理, 2017, 46(7): 416. doi: 10.7693/wl20170702 CHENG S, CHEN J, WANG L. Physic, 2017, 46(7): 416. (in Chinese) doi: 10.7693/wl20170702 [22] LECUN Y, BENGIO Y, HINTON G. Nature, 2015, 521(7553): 436. doi: 10.1038/nature14539 [23] PANG L G, ZHOU K, SU N, et al. Nat Commun, 2018, 9: 210. doi: 10.1038/s41467-017-02726-3 [24] WANG Z A, PEI J C, LIU Y. Phys Rev lett, 2019, 123: 122501. doi: 10.1103/PhysRevLett.123.122501 [25] LI F P, WANG Y J, LV H L, et al. J Phys G: Nucl Part Phys, 2020, 47: 115104. doi: 10.1088/1361-6471/abb1f9 [26] RABAN I, TONY M, HENRIK W, et al. Phys Rev lett, 2020, 124: 010508. doi: 10.1103/PhysRevLett.124.010508 [27] GIUSEPPE C, IGNACIO C, KYLE C, et al. Rev Mod Phys, 2019, 91: 045002. doi: 10.1103/RevModPhys.91.045002 [28] 李庆峰, 李祝霞, BLEICHER M, et al. 原子核物理评论, 2011, 28(2): 142. doi: 10.11804/NuclPhysRev.28.02.142 LI Q F, LI Z X, BLEICHERl M, et al. Nuclear Physics Review, 2011, 28(2): 142. (in Chinese) doi: 10.11804/NuclPhysRev.28.02.142 [29] 李庆峰, 王永佳, 郭琛琛, 等. 原子核物理评论, 2014, 31(03): 291. doi: 10.11804/NuclPhysRev.31.03.291 LI Q F, WANG Y J, GUO C C, et al. Nuclear Physics Review, 2014, 31(03): 291. (in Chinese) doi: 10.11804/NuclPhysRev.31.03.291 [30] WANG Y J, GUO C C, LI Q F, et al. Phys Rev C, 2014, 89: 034606. doi: 10.1103/PhysRevC.89.034606 [31] AICHELIN J. Physics reports, 1991, 202: 233. doi: 10.1016/0370-1573(91)90094-3 [32] SRIVASTAVA N, GEOFFREY E H. J Mach Learn Res, 2014, 15(1): 1929. [33] SERGEY I, CHRISTIAN S. In ICML, 2015(2). [34] KE G, MENG Q, FINLEY T, et al. LightGBM: A Highly Efficient Gradient Boosting Decision Tree[C]//VON LUX-BURG U, GUYON I, BENGIO S, et al. Proceedings of the 31st International Conference on Neural Information Processing Systems, Dec 4-9, 2017, Long Beach, CA, USA. New York: Curran Associates Inc, 2017: 3146. [35] LightGBM[EB/OL]. [2020-03-02]. https://lightgbm.readthedocs.io/en/latest/index.html. [36] ZEILER M D , FERGUS R. arXiv:1311.2901v3 [cs.CV]. -





 下载:
下载:











































































 甘公网安备 62010202000723号
甘公网安备 62010202000723号