-
The constituent quark effective degrees of freedom have made great successes in organizing hadron spectra where mesons are composed of quark-antiquark and baryons are made of three quarks[1-2]. While the strong interactions between quarks or quark-antiquark are accounted for by quantum chromodynamics (QCD), our knowledge of its property in the non-perturbative regime is still far from satisfactory. Hadrons, as a composite system of quarks and gluons, can only become stable if they are in a color singlet. This constraint makes it interesting to perceive the existence of more sophisticated objects, the so-called "QCD exotics", beyond the
$ q\bar{q} $ or$ qqq $ scenario, such as tetraquark ($ qq\bar{q}\bar{q} $ ), pentaquark ($ qqqq\bar{q} $ ), or hadronic molecule state (hadron as a bound state of two or more color-singlet hadrons). Undoubtedly, confirmation of such exotic hadrons will deepen our insights into the nature of QCD.During the past years significant progresses have been achieved in experiment. With the availabilities of high statistic data from BaBar, Belle, CLEO-c, BESIII, and LHCb, strong evidences for exotic hadrons have been observed (see Ref. [3] for a recent review). An apparent feature is that these exotic candidates cannot be easily accommodated into the successful quark-model predicted spectra. Moreover, some states have unexpected production or decay modes which are not favored by conventional quark structures. Among these candidates the early case
$ X(3872) $ sits at the threshold of$ D^*\bar{D} $ with$ J^{PC} = 1^{++} $ and has a mass much lower than the quark-model predicted$ \chi_{c1}(2P) $ state. The most direct evidence came from the observations of charged heavy-quarkonium-like states, such as$ Z_c(4430) $ ,$ Z_b(10610) $ and$ Z_b(10650) $ at Belle,$ Z_c(3900) $ at BESIII, Belle and CLEO-c, and$ Z_c(4020) $ at BESIII. These are indications for the missing pieces of information about the non-perturbative strong interaction dynamics, and have initiated a lot of efforts on both experiment and theory. Strong evidence for exotic baryons came from the LHCb experiment. In 2015 two possible heavy pentaquark candidates$ P_c(4380) $ and$ P_c(4450) $ , which decayed into$ J/\psi p $ , were reported in$ \Lambda_b\to J/\psi p K^- $ [4] by LHCb. While their quantum numbers could not be well determined based on the LHC Run-1 data, the updated analysis including the Run-2 data[5] suggests more refined structures in the invariant mass spectrum of$ J/\psi p $ . It shows that these narrow enhancements are closely correlated with the nearby$ S $ -wave thresholds.To be brief with the present experimental status for the search for exotic hadrons, it is quite surprising and interesting to note the following observations in the heavy quarkonium mass regions: (i) All the states below open thresholds are consistent with the description of potential quark models. (ii) Most of these exotic candidates, which obviously deviate from the potential model predictions, have masses located in the vicinity of some
$ S $ -wave open thresholds and their couplings turn out to be sizeable. (iii) The signals for charged heavy quarkonium states are indications for novel phenomena beyond the conventional quark model, but their structures are not indisputably established. In fact, it seems we are facing an apparent paradox: On the one hand, the multiquark structures would lead to much more profound hadron spectra and a tremendously large number of states are to be discovered by experiment. On the other hand, the number of states that so far we have observed is much smaller than one would have expected.There are some general questions to be answered: What causes the deviations of mass locations above the open thresholds? If there is a mechanism accounting for such phenomena, should it also have impact on the states below threshold? Then, it would be natural to question, what kind of observables could be sensitive to such a mechanism? And what are the reliable criteria accounting for their structures?
In this brief review we do not intend to give answers to these questions since an indisputable answer certainly is unavailable. However, to think about these questions may help work out a way towards the correct answer. Keeping these in mind, we would try to understand some more detailed and direct questions as an initiative for the field.
As follows, we first give a brief review of the main ingredients of the quark model, and then introduce the open threshold phenomena which will add important dynamics to the effective degrees of freedom inside hadrons. We will point out the special role played by the triangle singularity mechanism as a novel phenomena of threshold effects. Then, a discussion on the
$ X(3872) $ and$ Z_c(3900) $ is presented as a demonstration of the connection between threshold phenomena and exotic candidates. Brief remarks and prospects will be given in the last Section. -
The nonrelativsitic potential quark model has different versions while the essential ingredients are the same[6]. With the explicit introduction of the constituent quark degrees of freedom the conventional quark model has described a broad scope of phenomena of hadron spectroscopy. One bold assumption made for the quark potential is the one-gluon exchange (OGE) type of interaction. This is because the OGE interaction is literally a short-ranged interaction and it is unexpected to contribute dominantly to physics of non-perturbative scale. In those conventional quark models the OGE potential introduces the short-ranged Coulomb-type spin-independent interaction, spin-spin interaction, and spin-orbital interactions in association with the long-ranged confinement potential. A typical quark model Hamiltonian[7] is written as
$$ \begin{array}{l} H|\Psi\rangle = (H_0+\sum\limits_{i\neq j}V_{ij})|\Psi\rangle = E|\Psi\rangle \ , \end{array} $$ (1) with
$$ \begin{split} H_0\equiv \sum_i({ p}_i^2+m_i^2)^{1/2}\simeq \sum\limits_i\left(m_i+\frac{{ p}_i^2}{2m_i}\right) \ , \end{split} $$ (2) and
$$ \begin{array}{l} V_{ij}\equiv H_{ij}^{\rm conf}+H_{ij}^{\rm hyp}+H_{ij}^{\rm SO}+H_A \ , \end{array} $$ (3) where
$$ \begin{split} H_{ij}^{\rm conf} = & -\left[\frac{3}{4}(c+b r_{ij})-\frac{\alpha_s(r_{ij})}{r_{ij}}\right]{ F}_i\cdot{ F}_j \\ H_{ij}^{\rm hyp} =& -\frac{\alpha_s(r_{ij})}{m_im_j}\left\{\frac{8\pi}{3}{ s}_i\cdot{ s}_j\delta^3({ r})+\right.\\&\left.\frac{1}{r_{ij}^3}\left[\frac{3{ s}_i\cdot{ r}{ s}_j\cdot{ r}}{r_{ij}^2}-{ s}_i\cdot{ s}_j\right]\right\}{ F}_i\cdot{ F}_j \\ H_{ij}^{\rm SO}\equiv & H_{ij}^{\rm SO(cm)}+H_{ij}^{\rm SO(Tp)} \ . \end{split} $$ (4) In the above equation the spin-orbital coupling potential is decomposed into the c.m. contribution and Thomas processing contribution:
$$ \begin{split} H_{ij}^{\rm SO} = & -\frac{\alpha_s(r_{ij})}{r_{ij}^3}\left[\frac{1}{m_i}+\frac{1}{m_j}\right]\left[\frac{{ s}_i}{m_i}+\frac{{ s}_j}{m_j}\right]\cdot { L} \ { F}_i\cdot{ F}_j \ ,\\ H_{ij}^{\rm SO(Tp)} =& -\frac{1}{r_{ij}}\frac{\partial H_{ij}^{\rm conf}}{\partial r}\left[\frac{{ s}_i}{m_i^2}+\frac{{ s}_j}{m_j^2}\right]\cdot { L} \ . \end{split} $$ (5) The color operator
$ { F}_i\cdot{ F}_j $ contributes as an overall factor and has averaged values$ \langle { F}_i\cdot{ F}_j\rangle = -4/3 $ in a meson and$ -2/3 $ in a baryon.The above nonrelativistic Hamiltonian has been applied to both heavy and light quark system in the literature and the success was impressive. However, the connection between the quark model phenomenology and QCD is not obvious at all. Notice that the Hamiltonian in the heavy quark limit will be dominated by the static part
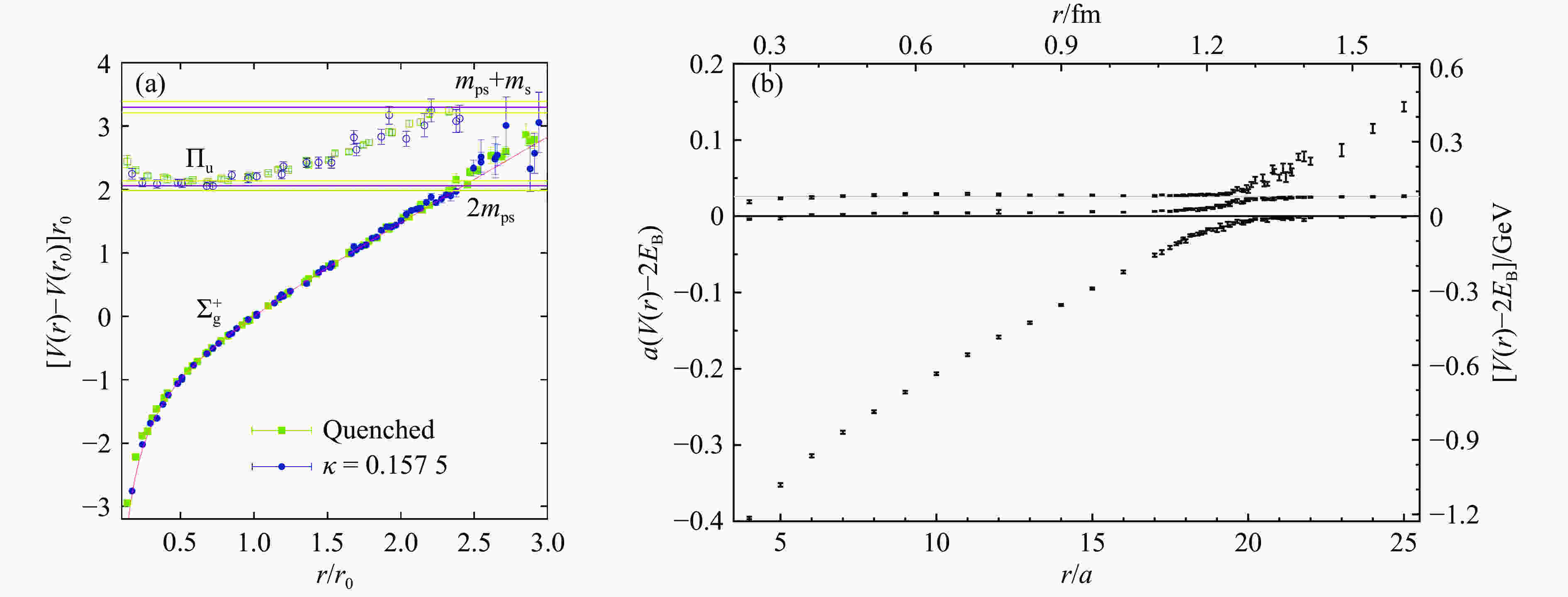
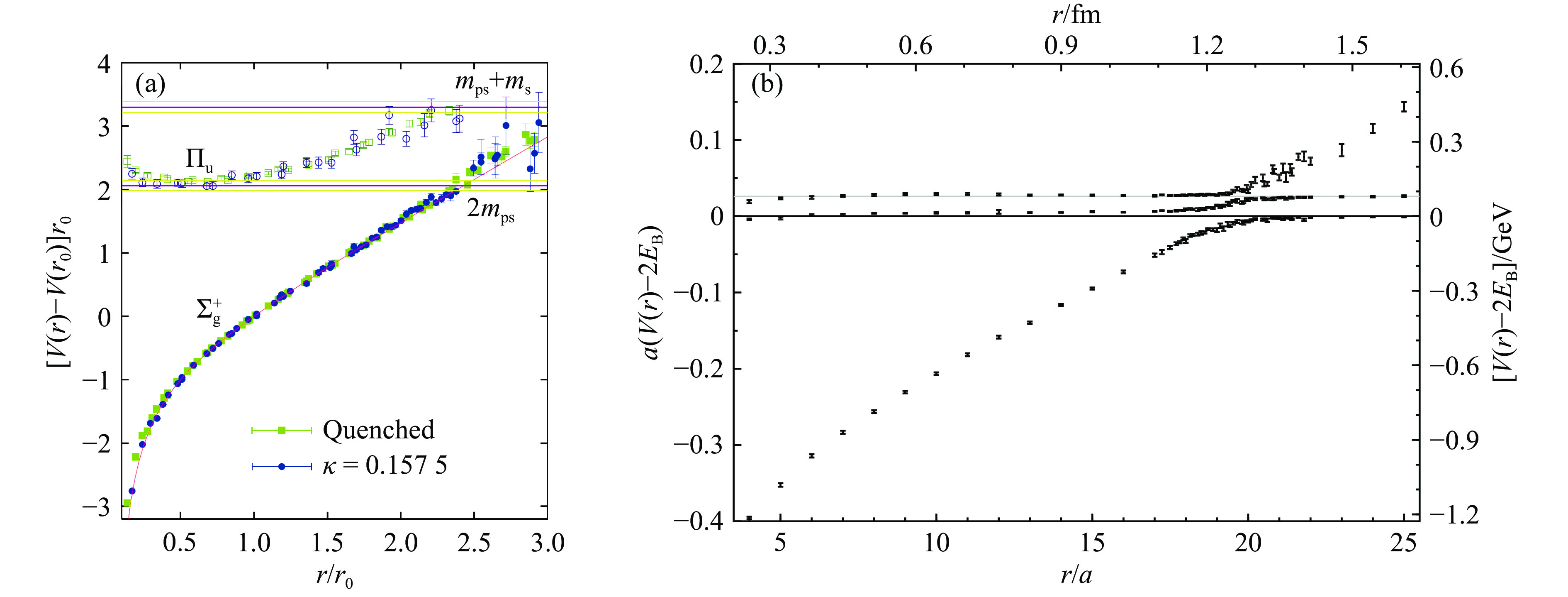
$ H_{ij}^{\rm conf} $ while the spin-spin and spin-orbital parts will be suppressed. In this sense the potential quark model in the heavy quark limit may provide a mimic of the soft QCD behavior where the heavy quark (antiquark) potentials can be investigated by Lattice QCD simulations[8] (see Ref. [9] for a review).In Ref. [8] an quenched lattice QCD calculation of the static potentials between heavy quarks and quark-antiquark suggests that the potential in a color-singlet indeed behaves a similar way as the spin-independent
$ H_{ij}^{\rm conf} $ in the quark model (see the left panel of Fig. 1). Namely, the short-ranged interaction manifests the Coulomb-type behavior from the OGE and the long-ranged part has a linear$ r_{ij} $ dependence[8]. This actually justifies the eigenstates extracted from the quark model approaches. However, one should keep in mind that these solutions can only be treated as the leading order approximation since they are orthogonal states which literally would not decay at all. Consider that physical states with sufficiently large masses have widths and can decay strongly into channels involving light quarks, namely, the open channels. It means that the open channel contributions are important dynamics which however are missing in the potential quark model prescription for hadrons.The inclusion of the open-channel contributions will lead to breakdown of the conventional quark model potential. This was recently demonstrated by the unquenched LQCD simulation. In Ref. [10] it was shown that the open threshold actually levels off the linear potential at large distance (see the right panel of Fig. 1). Meanwhile, a color octet part becomes color singlet and then follows the linear confinement behavior. Phenomenologically, it means that the creation of a pair of light
$ q\bar{q} $ from the nontrivial vacuum of QCD via the string breaking has provided a color screening for the existing heavy quark and antiquark to form two color-singlet objects (say a charmonium state decaying into two charmed mesons).The impact of open channel contributions on the hadron spectroscopy① has been broadly investigated in the literature[11-15]. In particular, the
$ S $ -wave open thresholds seem to be crucial for understanding those observed near-threshold exotic hadron candidates. In fact, there have been a lot of studies proposing that some of those states should be hadronic molecules which are bound states of the constituent hadrons to which they have the strongest coupling. A recent review of the hadronic molecule scenario can be found in Ref. [16]. One can also find reviews on other possible scenarios for exotic hadrons in Refs. [17-20]. As emphasized earlier that this brief review is advocated to identifying a minimum set of dynamical ingredients needed for accommodating the present experimental observations, thus, we only focus on a number of novel features arising from these threshold phenomena. -
Weinberg's compositeness theorem provides a handle for understanding the structure of near-threshold states on the basis of effective field theory (EFT)[21-23]. The basic idea is to introduce the long-ranged interaction potential between two
$ S $ -wave hadrons which can bind these two constituent hadrons and lead to the near-threshold pole structure in the scattering amplitude below the open threshold. A necessary condition or a unique feature is that these constituent hadrons should be stable (narrow) particles. Thus, they can propagate almost on shell such that the hadronic degrees of freedom can be recognized in the wavefunction. Quantum mechanically the hadronic degrees of freedom correspond to the long-distance part of the wavefunction where the constituents are well separated. Such a scale is described by the size parameter$ R\sim 1/\gamma = 1/\sqrt{2\mu E_{\rm B}} $ , where$ \mu\equiv m_{h_1}m_{h_2}/(m_{h_1}+m_{h_2}) $ is the reduced mass and$ E_{\rm B}\equiv -(E-m_{h_1}-m_{h_2}) $ is the binding energy. Quantity$ \gamma $ is the typical momentum scale for the constituent hadrons. It is possible that such a long-range structure can mix with the so-called "elementary" part of the wavefunction in a physical state② due to the strong coupling between the constituent hadrons and the elementary state. A detailed review of the definition for hadronic molecules can be found in Ref. [16]. Here we only outline the essence of an EFT prescription of such exotic objects.By extending the QM Hamiltonian
$ H $ in Eq. (1) to include the couplings of orthogonal states to the continuum, one can express the eigen equation as$$ \begin{array}{l} H|\Psi\rangle = \left( \begin{array}{cc} H_c & V \\ V & \tilde{H}^0_{hh} \end{array}\right)|\Psi\rangle = E|\Psi\rangle \ , \end{array} $$ (6) where
$ H_c $ corresponds to the quark model Hamiltonian and$ \tilde{H}^0_{hh} = m_{h_1}+m_{h_2}+|{ k}|^2/2\mu $ denotes the sum of the mass and kinetic energy of the two-hadron system③;$ V $ denotes the transition operator for the QM eigenstate coupling to the two-body continuum state; and$ |\Psi\rangle $ denotes the wavefunction of the physical state which is a linear superposition of the short-range QM eigenstates ($ |\Psi_0\rangle $ ) and the long-range component of the two-hadron system ($ |h_1h_2\rangle $ ):$$ \begin{array}{l} |\Psi\rangle = \left( \begin{array}{c} \lambda|\Psi_0\rangle\\ \chi({ k})|h_1h_2\rangle \end{array} \right) \ . \end{array} $$ (7) In the above equation
$ \lambda $ is the probability amplitude of the short-distance component in the physical state, and$ \lambda^2 $ is the corresponding probability. By defining$ \langle\Psi_0|V|h_1h_2\rangle\equiv f({ k}) $ and substituting the above wavefunction into Eq. (6), one has$$ \begin{split} \lambda = \chi({ k})\frac{\langle\Psi_0|V|h_1h_2\rangle}{E-E_c} \ , \end{split} $$ (8) $$ \begin{split} \chi = \lambda\frac{\langle h_1h_2|V|\Psi_0\rangle}{E-m_{h_1}-m_{h_2}-|{ k}|^2/(2\mu)} \ , \end{split} $$ (9) where
$ E_c $ (containing the constituent masses) is the eigenvalue of the short-ranged wavefunction that can be related to the eigenvalue of e.g. Eq. (1). Although the above two relations can both help determine the structure of the physical state, technically speaking, Eq. (8) would depend on our knowledge about the short-range Hamiltonian since Hamiltonians such as Eq. (1) are always model-dependent. In contrast, Eq. (9) can be better controlled with the essence of the EFT[21-22].By defining the binding energy
$ E_{\rm B}\equiv -(E- m_{h_1}-m_{h_2}) $ and with the normalization condition, one arrives at$$ \begin{split} \langle\Psi|\Psi\rangle = \lambda^2\left\{1+\int\frac{{\rm d}{ k}}{(2\pi)^3}\frac{\langle\Psi_0|V|h_1h_2\rangle^2}{[E_{\rm B}+|{ k}|^2/(2\mu)]^2} \right\} = 1 \ , \end{split} $$ (10) where the integral is the energy derivative of the self energy represented by the two-point loop function and
$ \lambda^2 $ is actually the wavefunction renormalization constant of the hadron. Note that the integral takes a positive value for the case of a bound state. It thus leads to a probability interpretation for$ \lambda^2 $ as the probability for finding the physical state in an elementary state (driven by the short-ranged dynamics) or$ (1-\lambda^2) $ as the probability for finding the physical state in a hadronic molecular state (driven by the long-ranged dynamics).For near-threshold phenomena the probability interpretation becomes problematic if the poles appear on the second Riemann sheet (the nearest unphysical sheet to the physical one). In such a case the two-point loop function is no longer a real number and the states cannot be normalized. However, the observables can still be affected strongly by the poles when they are close enough to the physical one. Namely, the hadronic degrees of freedom inside such states can manifest themselves in observables. Thus, the concept of hadronic molecules is actually extended. Further discussions on the extension of the Weinberg's compositeness theorem can be found in the literature (see Ref. [16] and references therein).
The integral in Eq. (10) converges if the coupling function
$ \langle\Psi_0|V|h_1h_2\rangle $ is a constant, i.e.$ g_0\equiv \langle\Psi_0|V| h_1h_2\rangle $ . This occurs as a good approximation for an$ S $ -wave coupling with the interaction range much smaller than the size of the molecular state. Using$ \beta $ to denote the inverse of the interaction range, it means$ \beta >> \gamma $ . One then arrives at$$ \begin{split} 1 = \lambda^2\left[1+\frac{\mu^2 g_0^2}{2\pi\sqrt{2\mu E_{\rm B}}}+{\cal O}\left(\frac{\gamma}{\beta}\right)\right] \ . \end{split} $$ (11) Or, it can be expressed as
$$ \begin{split} g_{\rm eff}^2\equiv \lambda^2 g_0^2 = \frac{2\pi\gamma}{\mu^2}\big(1-\lambda^2\big) \ , \end{split} $$ (12) where
$ g_{\rm eff} $ is the coupling for the physical state to the continuum. This relation allows the definition of the wavefunction renormalization constant$ Z\equiv \lambda^2 $ . It relates the physical coupling constant to the probability of finding the state in an elementary configuration ($ Z $ ) or in a molecular one ($ 1-Z $ ).The presence of the nearby open threshold continuum naturally requires a renormalization of the bare state propagator via the self-energy corrections. The physical propagator can then be extracted by the two-state scattering amplitude. It will redefine the wavefunction renormalization constant
$ Z $ at the physical pole in the NREFT[24-25]. To save space, we refer readers to Ref. [16] for details about the extraction of physical observables in the NREFT framework. -
Apart from the possible existence of hadronic molecular states near threshold, there could also be leading contributions arising from the open-threshold phenomena even without a genuine pole structure present. This is referred to the kinematic ''triangle singularity''(TS) mechanism which has initiated a lot of discussions in the study of hadron spectroscopy.
The TS mechanism is also known as ''Landau singularity''[26] which describes a singular property of a triangle loop amplitude caused by a special on-shell kinematic condition. In Fig. 2 a typical triangle diagram is shown with kinematic variables. Without losing generality the corresponding scalar loop function can be expressed by the Feynman parametrization:
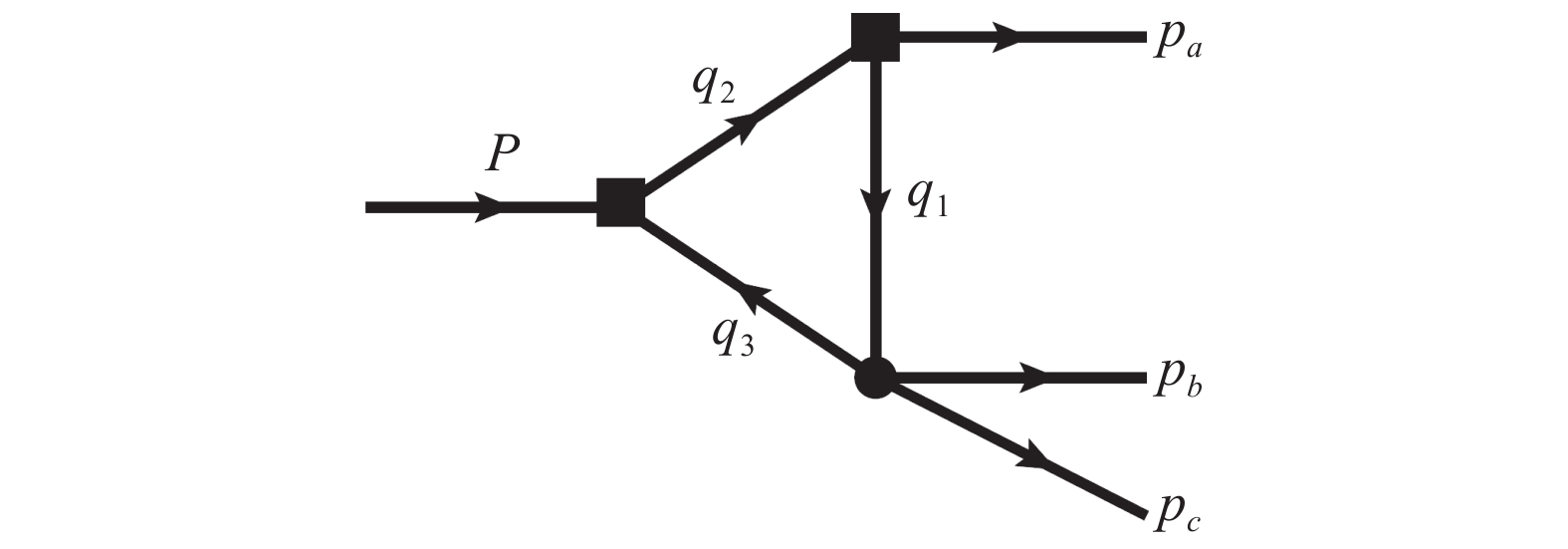
Figure 2. Illustration of the three-body decay of a hadron via the triangle loop diagram. The internal masses are
$m_i^2=q_i^2$ and the external kinematic variables are defined as$P^2=s_1$ ,$(p_b+p_c)^2=s_2$ , and$p_a^2=s_3$ $$ \begin{split} & \quad I(s_1,s_2,s_3) \\& =\frac{1}{i(2\pi)^4}\int \frac{{\rm d}^4 q_1}{(q_1^2-m_1^2+i\epsilon)(q_2^2-m_2^2+i\epsilon)(q_3^2-m_3^2+i\epsilon)} \\ & =\frac{-1}{16\pi^2}\int_0^1 \int_0^1 \int_0^1 {\rm d}a_1\ {\rm d}a_2\ {\rm d}a_3\ \frac{\delta(1-a_1-a_2-a_3)}{D-i\epsilon} \ , \end{split} $$ (13) where
$$ \begin{split} D \equiv \sum\limits_{i,j = 1}^{3} a_i a_j Y_{ij}, \ \ Y_{ij} = \frac{1}{2} \left[ m_i^2+m_j^2-(q_{i}-q_{j})^2 \right] \ .\nonumber \end{split} $$ The TS kinematics corresponds to such a necessary condition when all the internal particles approach their on-shell conditions simultaneously within the physical boundary. Mathematically, it can be constrained by the Landau equation,
$ \partial D / \partial a_j = 0 $ , which leads to:$$ \begin{array}{l} \rm{det}[Y_{ij}] = 0 \ , \end{array} $$ (14) where
$ \rm{det}[Y_{ij}] $ is a function including three external invariant masses$ \sqrt{s_i} $ and three internal masses$ m_i $ ($ i = 1,2,3 $ ).By fixing the internal masses
$ m_i $ and the external invariants$ s_1 $ and$ s_3 $ , one obtains the solutions of Eq. (14) for$ s_2 $ , i.e.,$$ \begin{split} s_2^{\pm} =& (m_1+m_3)^2+\frac{1}{2m_2^2} {\big[}(m_1^2+m_2^2-s_3)\\&(s_1-m_2^2-m_3^2)-4m_2^2 m_1 m_3 \\ & \pm \lambda^{1/2}(s_1,m_2^2,m_3^2)\lambda^{1/2}(s_3,m_1^2,m_2^2){\big ]}, \end{split} $$ (15) with
$ \lambda(x,y,z)\equiv (x-y-z)^2-4yz $ . Likewise, by fixing$ m_i $ ,$ s_2 $ and$ s_3 $ one obtains the solutions for$ s_1^\pm $ , i.e.,$$ \begin{split} s_1^{\pm} =& (m_2+m_3)^2+\frac{1}{2m_1^2} {\big[}(m_1^2+m_2^2-s_3)\\&(s_2-m_1^2-m_3^2)-4m_1^2 m_2 m_3 \\ & \pm \lambda^{1/2}(s_2,m_1^2,m_3^2)\lambda^{1/2}(s_3,m_1^2,m_2^2){\big ]}. \end{split} $$ (16) Within the physical boundary only the solution of
$ s_1^- $ or$ s_2^- $ corresponds to the TS condition as discussed in details in Refs. [26-27].To see the leading contributions from the TS mechanism, one can take the single dispersion representation of
$ I(s_1,s_2,s_3) $ in$ s_2 $ [28-32]:$$ \begin{split} I(s_1,s_2,s_3) = \frac{1}{\pi}\int_{(m_1+m_3)^2}^{\infty} \frac{{\rm d}s_2^\prime}{s_2^\prime -s_2 -i\epsilon}\ \sigma(s_1,s_2^\prime,s_3) \ , \end{split} $$ (17) where
$ \sigma(s_1,s_2,s_3) $ is the spectral function and can be obtained by the Cutkosky's rules[33]:$$ \begin{split} \sigma(s_1,s_2,s_3) = & \frac{-1}{16\pi}\int_0^1 \int_0^1 \int_0^1 {\rm d}a_1\ {\rm d}a_2\ {\rm d}a_3\ \delta(1-\\& a_1-a_2-a_3) \delta(D) \ , \end{split} $$ (18) which results in
$$ \begin{array}{l} \sigma(s_1,s_2,s_3) = \sigma_+ - \sigma_-, \end{array} $$ (19) with
$$ \begin{split} \sigma_{\pm}(s_1,s_2,s_3) =& \frac{-1}{16\pi \lambda^{1/2}(s_1,s_2,s_3)} \rm{log}\big[-s_2(s_1+\\&s_3-s_2+m_1^2+m_3^2-2m_2^2)- \\ &(s_1-s_3)(m_1^2-m_3^2) \pm \lambda^{1/2}(s_1,s_2,s_3)\\&\lambda^{1/2}(s_2,m_1^2,m_3^2)\big]. \end{split} $$ (20) One can see that for the fixed
$ s_1 $ ,$ s_3 $ and$ m_i $ , the spectral function$ \sigma(s_1,s_2,s_3) $ has logarithmic branch points$ s_2^\pm $ given by solving the Landau equation (Eq. (14)). As shown in Ref. [34], two singularities of the integrand in Eq. (17), i.e.$ s_2^- $ and$ s_2+i\epsilon $ , will pinch the contour of integration in the$ s_2^\prime $ -plane, and this is a direct manifestation of the TS as the leading singularity in$ I(s_1,s_2,s_3) $ .As the TS enhancement is closely associated with the thresholds of interest, it actually introduces rich but sometimes mysterious phenomena to threshold enhancements. Some of the key features can be itemized as follows[35]:
● Although the TS mechanism arises from the special kinematic condition for the triangle loop (we restrict to the scalar loop as an example), it unavoidably involves dynamics. For different decay processes the structure of the triangle loop will depend on the vertex couplings. For instance, in Refs. [35-36] it was shown that under the TS condition the scalar loop contribution is only part of the loop amplitude. However, we emphasize that the TS contribution should contain all the triangle loop amplitudes instead of the scalar loop exclusively[35].
● The nonvanishing vertex couplings suggest that the intermediate particle (e.g. particle 2 in Fig. 2) should have a width. As a consequence the logarithmic divergence will become limit and the TS contribution will become milder. A systematic treatment of the width effects by a complex mass was presented in Ref. [35].
● If the main contributions of a triangle loop amplitude is given by the TS mechanism, for some physical processes the motions of the internal particles could be treated nonrelativistically. Then, the scalar triangle loop can be directly integrated out, and the leading logarithmic singularity can be explicitly extracted. In particular, for nonrelativistic heavy meson loop transitions where the TS mechanism is present, the loop amplitudes can be analyzed in the nonrelativistic effective field theory (NREFT) framework and a power-counting scheme can be established[35].
● In contrast, for light hadron loop transitions sometimes the nonrelativistic approximation can hardly be justified, and analyses of the triangle loop in the Mandelstam representation should be more appropriate. For most cases an empirical form factor has to be included to cut off the ultraviolet divergence and model-dependence would be unavoidable. However, the absorptive part of the amplitude can still keep relatively model-independent[35,37].
Recognition of the presence of the TS mechanism in hadron productions and decays turns out to be crucial for our understanding various threshold phenomena. The first strong case manifesting the TS mechanism was proposed in Refs. [38-39]. Applications to physical processes can be found in Ref. [34] and two recent reviews[16,40].
-
As mentioned earlier, there are numerous newly observed enhancements located near some
$ S $ -wave open thresholds to which the couplings turn out to be sizeable. We make some general discussions on the emergence of threshold structures and some observed enhancements can be possibly interpreted as hadronic molecules.In the meson sector the lowest-lying "stable" particles are pseudoscalar (P) and vector (V) mesons. Their
$ S $ -wave couplings give access to quantum numbers which can be identified as candidates for hadronic molecules. For some of the low excitations, e.g. the first orbital excitation states, there also exist narrow states with which the strong$ S $ -wave couplings may give access to more quantum numbers. Whether a$ P $ -wave coupling can lead to hadronic molecular structures is still a question under debating. We will comment some issues concerning the$ P $ -wave interactions.In Table 1 the possible quantum numbers accessible via the "stable" states are listed. In the heavy meson sector there are candidates that can fit in the category. The observation of
$ X(3872) $ by Belle in 200[41] is often marked as the first evidence for exotic heavy-quarkonium-like states. Since then, a large number of the so-called "$ XYZ $ states" have been observed in experiment and initiated a lot of theoretical studies. See e.g. recent reviews and different theoretical interpretations therein[16-20]. As mentioned earlier, one interesting features with these$ XYZ $ states is that most of them are located near some$ S $ -wave open channels to which these states seem to have very strong couplings.Table 1. Quantum numbers accessible via the pseudoscalar, vector, and axial vector meson two-body interactions.
Two-body channel $ S $-wave ($ L = 0 $) $ P $-wave ($ L = 1 $) Open charm Open bottom PP $ 0^{+(\pm)} $ $ 1^{-(\pm)} $ $ D\bar{D} $ $ B\bar{B} $ PV $ 1^{+(\pm)} $ $ 0^{-(\pm)}, \ 1^{-(\mp)}, \ 2^{-(\pm)} $ $ D^*\bar{D}+c.c. $ $ B^*\bar{B}+c.c. $ VV $ 0^{+(+)} $ $ 1^{-(+)} $ $ D^*\bar{D}^* $ $ B^*\bar{B}^* $ $ 1^{+(-)} $ $ 0^{-(-)} $, $ 1^{-(-)} $, $ 2^{-(-)} $ $ 2^{+(+)} $ $ 1^{-(+)} $, $ 2^{-(+)} $, $ 3^{-(+)} $ PA $ 1^{-(-)} $ $ \dots\dots $ $ D\bar{D}_1+c.c. $ $ B\bar{B}_1+c.c. $ VA $ 0^{-(\pm)} $, $ 1^{-(\mp)} $, $ 2^{-(\pm)} $ $ \dots\dots $ $ D^*\bar{D}_1+c.c. $ $ B^*\bar{B}_1+c.c. $ As an example to demonstrate the threshold phenomena, we focus on the
$ D^*\bar{D}+c.c. $ threshold where two exotic candidates,$ X(3872) $ [41] and$ Z_c(3900) $ [42-44], have been observed in experiment. With their masses close to the$ D^*\bar{D}+c.c. $ threshold and the quantum numbers measured in experiment, i.e.$ (I^G, \ J^{PC}) = (0^+, \ 1^{++}) $ and$ (1^+, \ 1^{+-}) $ , respectively, they can couple to the$ D^*\bar{D}+c.c. $ via the following configurations with fixed$ C $ -parity:$$ \begin{split}& \frac{1}{\sqrt{2}}(D^*\bar{D}+D\bar{D}^*), ~~ {\rm{for}} \ X(3872), \\& \frac{1}{\sqrt{2}}(D^*\bar{D}-D\bar{D}^*), ~~{\rm{for}} \ Z_c(3900) \ . \end{split} $$ (21) Here,
$ \hat C {\cal M} = \bar{\cal M} $ is adopted for the$ C $ -parity transformation.Another advantage for the heavy meson system with a small binding energy is that it allows the implementation of the non-relativistice effective field theory (NREFT) approaches which are improvable order by order with the inclusion of local operators and pion exchanges, and the short-distance physics is encoded in the coefficients of the local operators. The compositeness theorem by Weinberg then connects the effective coupling constant of the physical state to the open channel continuum with the probability of finding the compact short-distance component in the wavefunction (see Eq. (12)).
The success of the EFT approaches can be recognized via the indication of a universality of the long-distance wavefunction which is insensitive to the binding mechanisms. It should be noted that the physical coupling,
$g_{\rm eff}^2\equiv\lambda^2 g_0^2 = \frac{2\pi\sqrt{2\mu E_{\rm B}}}{\mu^2}(1-\lambda^2)$ , suggests that there must be a short-distance component inside a hadronic molecular state given that$ E_{\rm B}> 0 $ . However, a quantitative determination of the short-distance dynamics is nontrivial. For a bound state the probability of finding the compact component in the physical wavefunction, i.e.$ \lambda^2 $ , is insufficient for disentangling the detailed dynamics since they are hard-scale physics which have been integrated out and absorbed into some unknown coefficients. Thus, observables sensitive to the short-distance physics thus should be identified and investigated.To be slightly specific here, we discuss some interesting threshold phenomena with the exotic candidates
$ X(3872) $ and$ Z_c(3900) $ . We skip details about the experimental status and theoretical models since one can refer to the recent reviews[16-20] and references therein, but only focus on some key points which turn out to be strongly associated with the threshold dynamics and kinematics, and need further attention or investigations. -
The strong attractive
$ S $ -wave interaction between$ D^{*}\bar{D}+c.c. $ was studied by Törnqvist and the$ X(3872) $ with$ (I^G, \ J^{PC}) = (0^+, \ 1^{++}) $ was literally predicted as a$ D^{*}\bar{D}+c.c. $ bound state which is an analogue of the deuteron[45] in a sense of the crucial role played by the long-ranged pion exchange potential. The mass of$ X(3872) $ almost sits at the$ D^{*0}\bar{D}^0+c.c. $ threshold with a small binding energy$ B_X = M_{D^0}+M_{D^{*0}}-M_X = 0.00\pm 0.18 $ MeV[46]. It makes$ X(3872) $ an ideal candidate for the hadronic molecule. In contrast, the potential quark model did not predict any state in such a mass region[6].The small binding energy, or large scattering length for the
$ S $ -wave$ D^{*0}\bar{D^0}+c.c. $ scattering implies a universality of the long-distance wavefunction of$ X(3872) $ to be insensitive to the binding mechanism. Effective field theories were developed to study the dynamics arising from the$ S $ -wave$ D^{*0}\bar{D^0}+c.c. $ scattering in association with the production and decays of$ X(3872) $ [47-50]. However, the case for the$ D^{*}\bar{D}+c.c. $ interactions should be significantly different from the proton-neutron long-range interactions since in the pion exchange potential for the$ D^{*}\bar{D}+c.c. $ interactions the exchanged pion can be on-shell and contribute to the potential with an imaginary part. This gives rise to a three-body cut in the scattering amplitude and makes the potential approximation for the pion exchange invalid[47-50]. A detailed review of the hadronic molecule interpretation of$ X(3872) $ can be found in Ref. [16].It is crucial that the quantum numbers of
$ X(3872) $ have been unambiguously determined as$ (I^G, \ J^{PC}) = (0^+, \ 1^{++}) $ . This makes it natural to include the$ S $ -wave open channel contributions and allows a separation of different energy scales. Thus, the EFT approaches can be implemented.For scatterings between two heavy flavor mesons the heavy quark spin symmetry (HQSS) in the limit of infinitely large mass for the heavy quarks can be implemented. In the limit of infinitely large heavy quark mass the heavy quark spin will decouple from the light ones, thus, conserve in the scattering. For convenience, the heavy-light meson can be labelled by the total angular momentum carried by the light quark, i.e.
$ j^P $ , with$ { j} = { l}+{ s_q} $ and$ P $ for the meson parity. In the HQSS limit,$ D $ and$ D^* $ (similarly$ B $ and$ B^* $ ) form a spin doublet$ j^P = 1/2^- $ . Thus, the light quarks in the$ D^*\bar{D}+c.c. $ system with the relative orbital angular momentum$ { l} = 0 $ can form$ j^P = 0^+ $ and$ 1^+ $ .By assigning
$ X(3872) $ as a hadronic molecule of the$ D^{*0}\bar{D}^0+c.c. $ pair with$ (I^G, \ J^{PC}) = (0^+, \ 1^{++}) $ , it implies the possible existence of accompanying states in the multiplet of$ j = 1 $ with$ J^{PC} = 0^{++}, \ 1^{+-}, \ 2^{++} $ . However, note that such a scenario is only based on the HQSS. In reality, the HQSS is broken and more complicated phenomena are anticipated. Firstly, the$ D $ and$ D^* $ mass splitting will lead to different mass corrections in different channels. Secondly, the role played by the pion exchange potentials is different in different channels. For instance, the pion exchange is forbidden in the$ D\bar{D} $ channel. One need understand how crucial the pion exchange potential is in the formation of hadronic molecule states.Taking the pion exchange potential in the channel of
$ (I^G, \ J^{PC}) = (0^+, \ 1^{++}) $ for$ X(3872) $ as a reference, the light quarks couple to$ j = 1 $ , while the isospin is zero. This gives a sign constraint indicating the attractive pion exchange potential:$ \langle{ \sigma}_1\cdot { \sigma}_2\rangle \langle{ \tau}_1\cdot { \tau}_2\rangle = 1\times (-3) = -3 $ with$ ({ \sigma}_1+ { \sigma}_2)/2 = 1 $ and$ ({ \tau}_1+ { \tau}_2) = 0 $ . Note that$ { \sigma}_1 = 2{ s}_1 $ and$ { \sigma}_2 = { s}_2 $ are the Pauli operators for the interacting light quarks. If the pion exchange also provides an attractive potential for$ Z_c(3900) $ , it should require that$ ({ \sigma}_1+ { \sigma}_2)/ 2 = 0 $ , hence$ \langle{ \sigma}_1\cdot { \sigma}_2\rangle \langle{ \tau}_1\cdot { \tau}_2\rangle = (-3)\times 1 = -3 $ . However, one notices that in such a case$ Z_c(3900) $ belongs to the multiplet with$ j_l = 0 $ . Thus,$ Z_c(3900) $ and$ X(3872) $ cannot be connected with each other by the HQSS. This seems to be able to provide some hints about the production mechanisms for$ X(3872) $ and$ Z_c(3900) $ . Meanwhile, one notices that the$ 1^{+-} $ HQSS partner of$ X(3872) $ is generated by the$ D^*\bar{D}^* $ coupling which can be related to$ Z_c(4020/4025) $ observed in experiment. However, in this case the pion exchange provides a repulsive potential.An interesting consequence is that in the limit of the HQSS the
$ Z_c(3900) $ decays into$ \eta_c\rho $ will be suppressed. However, the recent BESIII measurement shows that the ratio of$ B.R.(Z_c^\pm(3900)\to \rho^\pm\eta_c)/ B.R.(Z_c^\pm(3900)\to J/\psi\pi^\pm) = 2.3\pm 0.8 $ [51], which seems to be contradicting with the expectation of the hadronic molecular picture. Such a conclusion needs to be cautioned because$ \rho $ meson is broad. The decay channel of$ Z_c^\pm(3900)\to \rho^\pm\eta_c $ will be affected significantly by the phase space correction due to the broad width of the$ \rho $ meson. Meanwhile, comparing the rescatterings between$ D^*\bar{D}+c.c.\to \rho\eta_c $ and$ J/\psi\pi $ by exchanging a$ D $ meson, one sees that the exchanged$ D $ meson can become highly off-shell in the$ J/\psi\pi $ channel due to the large mass difference between$ J/\psi $ and$ \pi $ . This will introduce more suppressions into the$ J/\psi\pi $ channel. In addition, the HQSS breaking allows the transition between$ D^*\bar{D}^* $ and$ D^*\bar{D}+c.c. $ and the$ \rho\eta_c $ channel may get further enhanced. Future detailed studies are needed to clarify these issues.The HQSS symmetry breaking also leads to isospin-breaking effects in
$ X(3872) $ decays into$ J/\psi\rho $ . Experimentally, the branching fraction,$ B.R.(X(3872)\!\to\! J/\psi\pi^+\pi^-\pi^0)/B.R.(X(3872)\to J/\psi\pi^+\pi^-)\simeq 1 $ , where the$ \pi^+\pi^-\pi^0 $ and$ \pi^+\pi^- $ are dominantly from the$ \omega $ and$ \rho^0 $ decays, respectively. This result can be understood by the large mass splitting between the$ D^{*0}\bar{D}^0+c.c. $ and$ D^{*+}D^-+c.c. $ thresholds and to both of them the physical state has large couplings. The isospin breaking effects can then be accounted for by the nonvanishing cancellation between the charged and neutral$ D^*\bar{D} $ loop amplitudes. In addition, the$ J/\psi\pi^+\pi^-\pi^0 $ channel is relatively suppressed by the phase space in comparison with the$ J/\psi\pi^+\pi^- $ . This measurement provides a strong evidence for the hadronic molecule interpretation for$ X(3872) $ .In the hadronic molecule scenario observables, which are driven by mechanisms involving the hadronic degrees of freedom, should be useful for probing the corresponding structures in the wavefunction. For instance, the strong decay of
$ X(3872)\to D^{0}\bar{D}^0\pi^0 $ should be dominated by the constituent$ D^{*0} $ decays into$ D\pi $ . The radiative decay of$ X(3872)\to D^{0}\bar{D}^0\gamma $ was also regarded as a probe of the long-distance wavefunction via the radiative decays of$ D^*\to D\gamma $ . However, one should be cautioned by the observation that the long-distance wavefunction contributes to the partial width via the$ M1 $ transition. In contrast, the transition of$ \chi_{c1}(nP)\to \gamma D\bar{D} $ can pick up a$ E1 $ transition operator followed by a strong vector charmonium coupling to$ D\bar{D} $ . So, a small short-distance component of$ c\bar{c} $ may contribute to the radiative decay the same order of magnitude as the long-distance component. This actually raises the question on the role played by the short-distance component of the$ X(3872) $ wavefunction[52]. Proper criteria which are sensitive to the underlying by mechanisms still need to be explored. -
The production mechanisms for both
$ X(3872) $ and$ Z_c(3900) $ have been explored in experiment and theory[16-20]. Instead of going through various model prescriptions, we again focus on some key issues which turn out to be closely related to the threshold phenomena.As candidates for the hadronic molecules the production mechanisms for these two states seem to be very controversial. An intuitive argument would be that their productions should be driven by the productions of their constituent hadrons, i.e.
$ D^*\bar{D}+c.c. $ , in order to feed the long-distance wavefunctions. Namely, their productions should be dominantly via the$ D^*\bar{D}+c.c. $ rescatterings. This argument is based on the wavefunction dominance of the long-distance component and the short-distance part is neglected. However, this is not the case in the production processes. One point to recognize this problem is that the virtual momentum for the charged$ D^*\bar{D}+c.c. $ pair is at the order of 120 MeV, which is lower than the typical$ \Lambda_{QCD} $ scale and should be explicitly considered. Some detailed discussions on the role of the short-distance component can be found in Ref. [16]. Here, we discuss the productions of$ X(3872) $ and$ Z_c(3900) $ in$ B $ meson decays to show that the short-distance component cannot be neglected.For
$ B\to D^*\bar{D}K $ via$ B\to X(3872)K $ the production mechanisms can be illustrated by Fig. 3[52]. The relevant Feynman rules for the$ X(3872) $ in the EFT can be set up following the scheme of Sec. 2.1. The propagator can be expressed as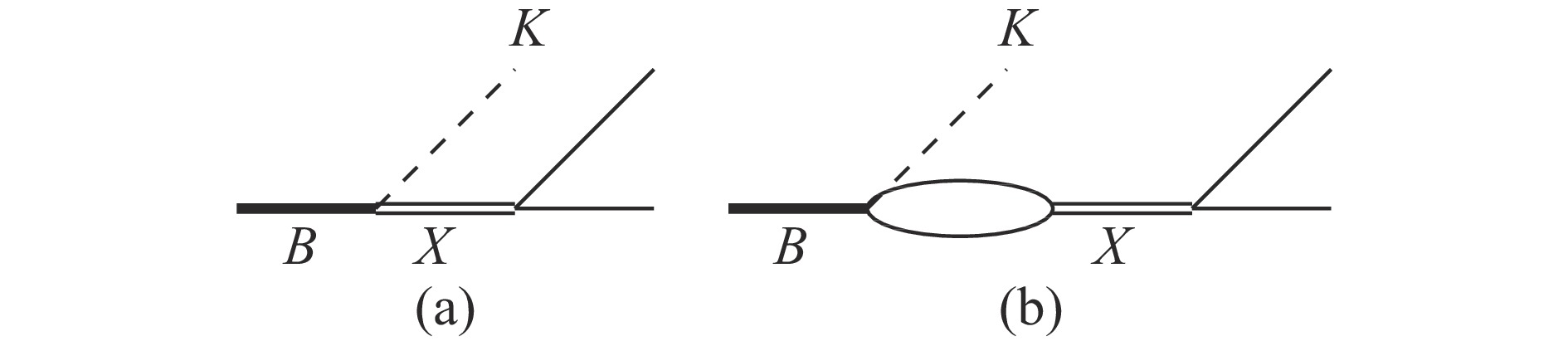
Figure 3. Leading diagrams for
$B\to X(3872)K\to $ $ D^{*0} \bar D^0 K$ [16]. The solid lines in the loop and final state represent the charm and anti-charm mesons$$ \begin{split} G(E)_X = \frac{iZ}{E+B+\tilde{\Sigma}^\prime(E)+i\Gamma/2}, \end{split} $$ (22) where
$ \Gamma $ denotes the non-$ D^{*0}\bar D^0 $ partial decay width of$ X(3872) $ . Note that a factor of$ \sqrt{2M_X} $ has been absorbed into the$ X(3872) $ field operator. In this convention a boson field has the dimension of$ 3/2 $ and the Feynman rule for an external boson is$ \sqrt{2M} $ . The vertex coupling for$ XD^{*0}\bar D^0 $ is given as$$ \begin{split} i\frac{g_0}{\sqrt{2}} = i(\frac{g^2}{2Z})^{1/2}, \end{split} $$ (23) where the factor
$ 1/\sqrt{2} $ is due to the definition of the$ C $ -even state$ (D^{*0}\bar D^0+D^0\bar D^{*0})/\sqrt{2} $ .The leading order transition amplitudes in Fig. 3 can be explicitly written as
$$ \begin{split} i{\cal{M}}_a =& -\frac{{\cal{A}}_{XK}}{\sqrt{2}}\frac{\sqrt{Z}g}{E+B+\tilde{\Sigma}^\prime(E)+i\Gamma/2}{ p}_K\cdot{ \epsilon}^*, \\ i{\cal{M}}_b =& {\cal{B}}_{DDK}\frac{\mu}{2\pi}\frac{g^2\sqrt{-2\mu E-i\epsilon}}{E+B+\tilde{\Sigma}^\prime(E)+i\Gamma/2}{ p}_K\cdot{\epsilon}^*, \end{split} $$ (24) where
$ { p}_K $ is the momentum of the$ K $ meson in the$ B $ meson rest frame;$ { \epsilon}^* $ is the polarization vector of the outgoing$ D^{*0} $ ;$ {\cal{A}}_{\rm XK} $ and$ {\cal{B}}_{\rm DDK} $ denote the production vertices$ B\rightarrow X(3872)K $ and$ B\rightarrow D^{*0}\bar D^0 K $ , respectively. Near the threshold of$ D^{*0}\bar D^0 $ , the two form factors$ {\cal{A}}_{\rm XK} $ and$ {\cal{B}}_{\rm DDK} $ are treated as constants.The relative strength between
$ {\cal{M}}_a $ and$ {\cal{M}}_b $ can be examined by the NREFT power counting. Note that near threshold the binding momentum$ \gamma = (2\mu B)^{1/2} $ and the three momentum of the charmed meson$ p $ are the same order, i.e.$ \gamma, \ p\sim{\cal{O}}(p) $ . Thus, we count$ E, \ B\sim{\cal{O}}(p^2) $ and$ g\sim {\cal{O}}(p^{1/2}) $ [24-25]. It leads to$ {\cal{M}}_a\sim{\cal{O}}(p^{-3/2}) $ and$ {\cal{M}}_b\sim{\cal{O}}(p^0) $ . From the power counting, one can see that the short-distant production mechanism is more important than the long-distance one. Interestingly, it should be noted that$ {\cal{M}}_a $ is proportional to the factor$ \sqrt{Z} $ . Therefore, it will be suppressed given that$ X(3872) $ is dominated by a molecular component. In the limit of$ Z\to 0 $ the term of$ {\cal{M}}_a $ will vanish. Then, the production of$ X(3872) $ will be via the long-distance production mechanism$ {\cal{M}}_b $ . As shown in Ref. [52], lineshape of the$ D^{*0}\bar{D}^0 $ spectrum in$ B\to D^{*0}\bar{D}^0 K $ is sensitive to the contributions from the short-distance production of$ {\cal{M}}_a $ . This feature naturally accounts for the short-distance production of hadronic molecules in various processes. See e.g. a similar analysis of the production of$ Y(4260) $ as a hadronic molecule of$ D_1(2420)\bar{D}+c.c. $ in$ e^+e^- $ annihilations[37,53-56].The production of
$ Z_c(3900) $ shares some similar features as$ X(3872) $ if it is a hadronic molecule. However, there are certain aspects that its production in$ B $ decays is different. In Fig. 4 we compare the production mechanisms for$ X(3872) $ and$ Z_c(3900) $ via (a) short-distance and (b) long-distance processes. Since$ Z_c(3900) $ is an isovector, its short-distance wavefunction (whatever it could be) cannot be produced directly. Only the long-distance process is allowed for its creation via the$ D^*\bar{D} $ scatterings. In contrast,$ X(3872) $ contains a short-distance component (e.g. a mixture of$ \chi_{c1}(2P) $ state) and a direct production via the$ c\bar{c} $ component is allowed and can be even dominant. This naturally explains why$ X(3872) $ is richly observed in high-energy production processes while$ Z_c(3900) $ so far has not been observed in the exclusive$ B $ decays.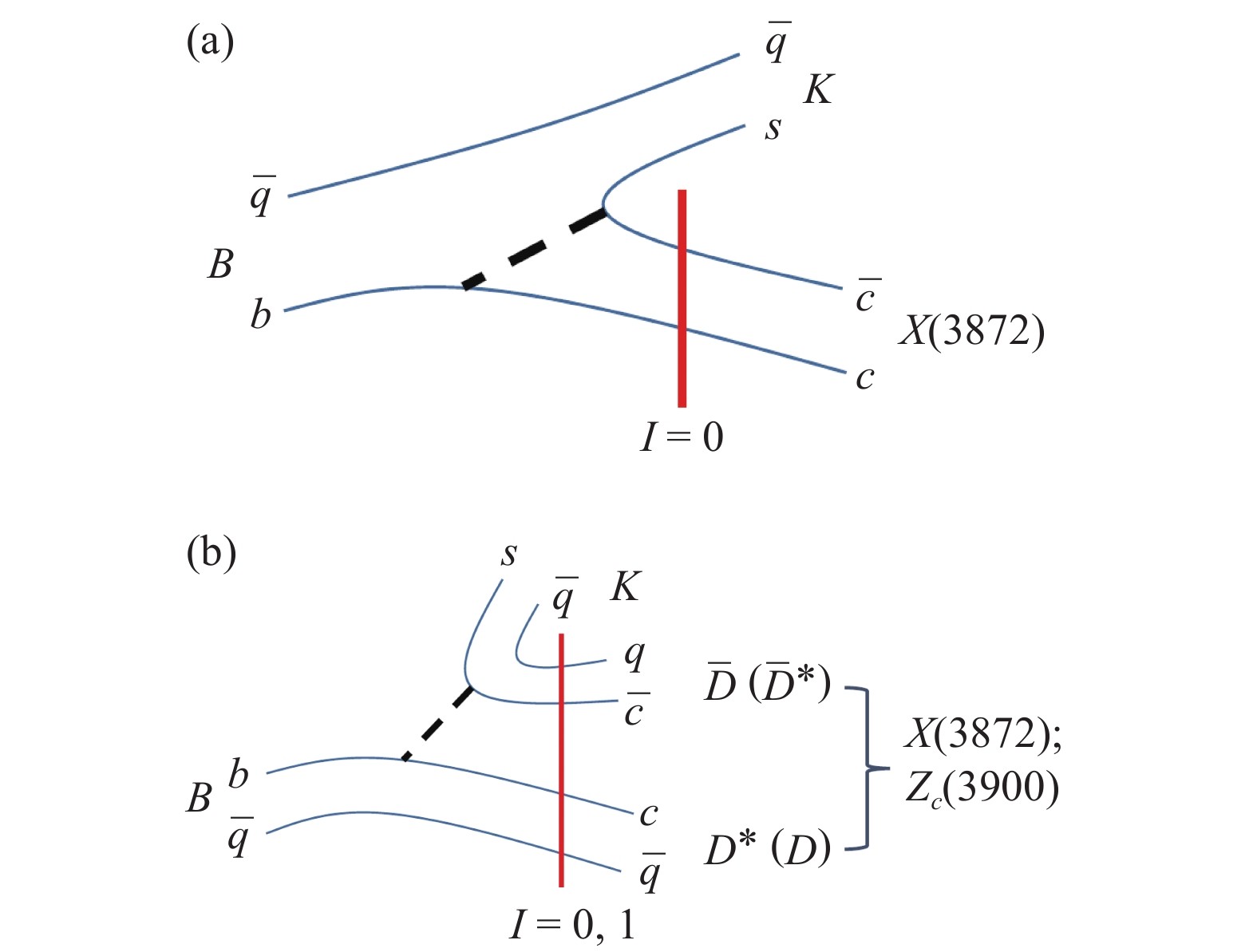
Figure 4. (color online) Schematic diagrams for the production of
$X(3872)$ and$Z_c(3900)$ in$B\to D^* {\bar D} K$ . The isoscalar short-distance component of$X(3872)$ allows its production directly via a$c\bar{c}$ configuration in (a) while both can be produced via the long-distance component of$D^*\bar{D}$ scatterings in (b)A novel phenomenon with the productions of
$ X(3872) $ and$ Z_c(3900) $ is associated with the role played by the TS mechanism. Being located in the vicinity of the$ D^*\bar{D}+c.c. $ threshold, these two states can be significantly affected by the TS mechanism in their productions. Following the observations of$ Z_c(3900) $ and$ Z_c(4020) $ in experiment[42-44,57], it was first proposed in Refs. [53,58] that the productions of these two states are closely related to the$ S $ -wave open thresholds,$ D_1(2420)\bar{D}+c.c. $ and$ D_1(2420)\bar{D}^*+ c.c. $ , in$ e^+e^- $ annihilations. These two thresholds have large couplings to the nearby charmonium-like states,$ Y(4260) $ and$ Y(4360) $ , which make it possible to interpret them as hadronic molecule states composed of these constituent hadrons. Furthermore, the productions of$ Z_c(3900) $ and$ Z_c(4020) $ via the decays of$ Y(4260) $ and$ Y(4360) $ will be enhanced by the TS mechanism. This phenomenon has been investigated by a series of works[37,53-56,58-60] which provide a self-consistent prescription of the so-far available experimental observables. It is interesting to note that it seems that all the present signals for$ Z_c(3900) $ are associated with the production of$ Y(4260) $ . Apart from those observed in$ e^+e^- $ annihilations, the D0 Collaboration observed$ Z_c(3900) $ in the decays of$ Y(4260) $ which are produced in semi-inclusive decays of$ b $ -flavored hadrons[61].Similar phenomenon was predicted by Ref. [62] where the TS mechanism plays an important role to enhance the production rate for
$ X(3872) $ in the energy region of$ Y(4260) $ in$ e^+e^- $ annihilations. It was later confirmed by the experimental data[63] which has provided very useful information about the structure of both$ X(3872) $ and$ Y(4260) $ . Recently, it was proposed by Ref. [64] to precisely measure the mass position of$ X(3872) $ in its productions via the TS mechanism. Although$ X(3872) $ has been confirmed in various processes and can be regarded as a well-established state, its mass position still has sizeable uncertainties. A precise measurement of its mass position is crucial for understanding its nature via the pole structure of the scattering amplitude in the energy complex plane. The intriguing idea of Ref. [64] will help experimentalists achieve a high-precision measurement of this quantity. -
In this proceeding we make a general review of threshold phenomena which are associated with many experimental observations of exotic candidates beyond the conventional quark model. We stress that the strong interactions between the open threshold hadrons can result in crucial changes to the quark potential in a quark model Hamiltonian and produce structures near threshold. Some of these structures can be accounted for as hadronic molecules depending on the analytic property of the scattering amplitudes in the complex energy plane. We also introduce the novel scenarios which are caused by the TS mechanism. This is a unique threshold phenomenon which was overlooked before, but turns out to be crucial for our understanding of those nontrivial threshold phenomena observed in experiment. As we know that, in principle, the QCD strong interaction could allow much richer hadron structures beyond the conventional quark model picture to exist, an unavoidable step towards a better understanding of the hadron spectroscopy is thus to understand the dynamics arising from the open thresholds. Future experimental data from BESIII, Belle, Belle-II, and LHCb, and progresses on LQCD may help gain a deeper insight into the nature of non-perturbative QCD.
Acknowledgement The author thanks collaborators for their contributions and discussions on the relevant studies presented in this proceeding. Financial support from the National Natural Science Foundation of China (11425525, 11521505), DFG and NSFC funds to the Sino-German CRC 110 "Symmetries and the Emergence of Structure in QCD" (11621131001), and National Key Basic Research Program of China under Contract(2015CB856700), are gratefully acknowledged.
-
摘要: 综述了量子色动力学奇特强子态研究中的一些热点问题,特别强调了有效理论研究强子分子态可以合理考虑阈效应和“三角奇异性”对近阈奇特强子态性质的重要影响,综合分析这些可能的机制可以帮助我们更好地理解强子谱。Abstract: We present a brief review of some topical issues in the study of QCD exotic hadrons. A special emphasis of the threshold phenomena is made by taking into account the implementation of the effective field theory study of hadronic molecules and the impact arising from the triangle singularity. A combined analysis may provide some clues towards a better understanding of the hadron spectroscopy.
-
Key words:
- Hadron physics /
- hadron spectroscopy /
- QCD exotics /
- hadronic molecule /
- threshold
Such states are often interpreted as the eigen-states of the potential quark model Hamiltonian which only involves the quark-quark or quark-antiquark interactions, namely, the short-ranged interactions.
Here, we keep the mass term in order to connect the nonrelativistic quark model eigenvalues to the eigenvalues of Hc.
-
Figure 3. Leading diagrams for
$B\to X(3872)K\to $ $ D^{*0} \bar D^0 K$ [16]. The solid lines in the loop and final state represent the charm and anti-charm mesonsFigure 4. (color online) Schematic diagrams for the production of
$X(3872)$ and$Z_c(3900)$ in$B\to D^* {\bar D} K$ . The isoscalar short-distance component of$X(3872)$ allows its production directly via a$c\bar{c}$ configuration in (a) while both can be produced via the long-distance component of$D^*\bar{D}$ scatterings in (b)Table 1. Quantum numbers accessible via the pseudoscalar, vector, and axial vector meson two-body interactions.
Two-body channel $ S $ -wave ($ L = 0 $ )$ P $ -wave ($ L = 1 $ )Open charm Open bottom PP $ 0^{+(\pm)} $ $ 1^{-(\pm)} $ $ D\bar{D} $ $ B\bar{B} $ PV $ 1^{+(\pm)} $ $ 0^{-(\pm)}, \ 1^{-(\mp)}, \ 2^{-(\pm)} $ $ D^*\bar{D}+c.c. $ $ B^*\bar{B}+c.c. $ VV $ 0^{+(+)} $ $ 1^{-(+)} $ $ D^*\bar{D}^* $ $ B^*\bar{B}^* $ $ 1^{+(-)} $ $ 0^{-(-)} $ ,$ 1^{-(-)} $ ,$ 2^{-(-)} $ $ 2^{+(+)} $ $ 1^{-(+)} $ ,$ 2^{-(+)} $ ,$ 3^{-(+)} $ PA $ 1^{-(-)} $ $ \dots\dots $ $ D\bar{D}_1+c.c. $ $ B\bar{B}_1+c.c. $ VA $ 0^{-(\pm)} $ ,$ 1^{-(\mp)} $ ,$ 2^{-(\pm)} $ $ \dots\dots $ $ D^*\bar{D}_1+c.c. $ $ B^*\bar{B}_1+c.c. $ -
[1] GELL-MANN M. Phys Lett, 1964, 8: 214. doi: 10.1016/S0031-9163(64)92001-3 [2] ZWEIG G. CERN-TH-401[R]. CERN, 1964. [3] OLSEN S L, SKWARNICKI T, ZIEMINSKA D. Rev Mod Phys, 2018, 90(1): 015003. doi: 10.1103/RevModPhys.90.015003 [4] AAIJ R, ADEVA B, ADINOLFI M, et al[LHCb Collaboration]. Phys Rev Lett, 2015, 115: 072001. doi: 10.1103/PhysRevLett.115.072001 [5] AAIJ R, BETETA C A, ADEVA B, et al[LHCb Collaboration]. Phys Rev Lett, 2019, 122: 22. doi: 10.1103/PhysRevLett.122.222001 [6] EICHTEN E, GOTTFRIED K, KINOSHITA T, et al. Phys Rev D, 1978, 17: 3090. doi: 10.1103/PhysRevD.17.3090,10.1103/physrevd.21.313.2 [7] GODFREY S, ISGUR N. Phys Rev D, 1985, 32: 189. doi: 10.1103/PhysRevD.32.189 [8] BALI G S, BOLDER B, EICKER N, et al[TXL and T(X)L Collaborations]. Phys Rev D, 2000, 62: 054503. doi: 10.1103/PhysRevD.62.054503 [9] BALI G S. Phys Rept, 2001, 343: 1. doi: 10.1016/S0370-1573(00)00079-X [10] BULAVA J, HÖRZ B, KNECHTLI F, et al. Phys Lett B, 2019, 793: 493. doi: 10.1016/j.physletb.2019.05.018 [11] EICHTEN E J, LANE K, QUIGG C. Phys Rev D, 2004, 69: 094019. doi: 10.1103/PhysRevD.69.094019 [12] BARNES T, SWANSON E S. Phys Rev C, 2008, 77: 055206. doi: 10.1103/PhysRevC.77.055206 [13] LI B Q, CHAO K T. Phys Rev D, 2009, 79: 094004. doi: 10.1103/PhysRevD.79.094004 [14] LI B Q, MENG C, CHAO K T. Phys Rev D, 2009, 80: 014012. doi: 10.1103/PhysRevD.80.014012 [15] LI B Q, CHAO K T. Commun Theor Phys, 2009, 52: 653. doi: 10.1088/0253-6102/52/4/20 [16] GUO F K, HANHART C, MEISSNER U G, et al. Rev Mod Phys, 2018, 90(1): 015004. doi: 10.1103/RevModPhys.90.015004 [17] CHEN H X, CHEN W, LIU X, et al. Phys Rept, 2016, 639: 1. doi: 10.1016/j.physrep.2016.05.004 [18] ESPOSITO A, PILLONI A, POLOSA A D. Phys Rept, 2017, 668: 1. doi: 10.1016/j.physrep.2016.11.002 [19] ALI A, LANGE J S, S STONE. Prog Part Nucl Phys, 2017, 97: 123. doi: 10.1016/j.ppnp.2017.08.003 [20] LIU Y R, CHEN H X, CHEN W, et al. Prog Part Nucl Phys, 2019, 107: 237. doi: 10.1016/j.ppnp.2019.04.003 [21] WEINBERG S. Phys Rev, 1963, 130: 776. doi: 10.1103/PhysRev.130.776 [22] WEINBERG S. Phys Rev, 1963, 131: 440. doi: 10.1103/PhysRev.131.440 [23] WEINBERG S. Phys Rev B, 1965, 137: 672. doi: 10.1103/PhysRev.137.B672 [24] KAPLAN D B, SAVAGE M J, WISE M B. Phys Lett B, 1998, 424: 390. doi: 10.1016/S0370-2693(98)00210-X [25] KAPLAN D B, SAVAGE M J, WISE M B. Nucl Phys B, 1998, 534: 329. doi: 10.1016/S0550-3213(98)00440-4 [26] LANDAU L D. Nucl Phys, 1959, 13: 181. doi: 10.1016/0029-5582(59)90154-3 [27] BONNEVAY G, AITCHISON I J R, DOWKER J S. Nuovo Cim, 1961, 21: 3569. [28] BARTON G, KACSER C. Nuovo Cim, 1961, 21: 3161. [29] FRONSDAL C, NORTON R E. J Math Phys, 1964, 5: 100. doi: 10.1063/1.1704053 [30] BRONZAN J B. Phys Rev B, 1964, 134: 687. doi: 10.1103/PhysRev.134.B687 [31] NORTON R E. Phys Rev B, 1964, 135: 1381. [32] LUCHA W, MELIKHOV D, SIMULA S. Phys Rev D, 2007, 75: 016001. doi: 10.1103/PhysRevD.75.016001 [33] CUTKOSKY R E. J Math Phys, 1960, 1: 429. doi: 10.1063/1.1703676 [34] LIU X H, OKA M, ZHAO Q. Phys Lett B, 2016, 753: 297. doi: 10.1016/j.physletb.2015.12.027 [35] DU M C, ZHAO Q. Phys Rev D, 2019, 100(3): 036005. doi: 10.1103/PhysRevD.100.036005 [36] ACHASOV N N, KOZHEVNIKOV A A, SHESTAKOV G N. Phys Rev D, 2015, 92(3): 036003. doi: 10.1103/PhysRevD.92.036003 [37] XUE S R, JING H J, GUO F K, et al. Phys Lett B, 2018, 779: 402. doi: 10.1016/j.physletb.2018.02.027 [38] WU J J, LIU X H, ZHAO Q, et al. Phys Rev Lett, 2012, 108: 081803. doi: 10.1103/PhysRevLett.108.081803 [39] WU X G, WU J J, ZHAO Q, et al. Phys Rev D, 2013, 87(1): 014023. doi: 10.1103/PhysRevD.87.014023 [40] GUO F K, LIU X H, SAKAI S. Progress in Particle and Nuclear Physics, 2020, 112: 103757. doi: 10.1016/j.ppnp.2020.103757 [41] CHOI S K, OLSEN S L, ABE K, et al[Belle Collaboration]. Phys Rev Lett, 2003, 91: 262001. doi: 10.1103/PhysRevLett.91.262001 [42] ABLIKIM M, ACHASOV M N, AI X C, et al[BESⅢ Collaboration]. Phys Rev Lett, 2013, 110: 252001. doi: 10.1103/PhysRevLett.110.252001 [43] LIU Z Q, SHEN C P, YUAN C Z, et al[Belle Collaboration]. Phys Rev Lett, 2013, 110: 252002. doi: 10.1103/PhysRevLett.110.252002 [44] XIAO T, DOBBS S, TOMARADZE A, et al. Phys Lett B, 2013, 727: 366. doi: 10.1016/j.physletb.2013.10.041 [45] TORNQVIST N A. Z Phys C, 1994, 61: 525. doi: 10.1007/BF01413192 [46] PATRIGNANI C, AGASHE K, AIELLI G, et al[Particle Data Group]. Chin Phys C, 2016, 40(10): 100001. doi: 10.1088/1674-1137/40/10/100001 [47] VOLOSHIN M B. Phys Lett B, 2004, 579: 316. doi: 10.1016/j.physletb.2003.11.014 [48] FLEMING S, KUSUNOKI M, MEHEN T, et al. Phys Rev D, 2007, 76: 034006. doi: 10.1103/PhysRevD.76.034006 [49] BRAATEN E, STAPLETON J. Phys Rev D, 2010, 81: 014019. doi: 10.1103/PhysRevD.81.014019 [50] JANSEN M, HAMMER H W, JIA Y. Phys Rev D, 2014, 89(1): 014033. doi: 10.1103/PhysRevD.89.014033 [51] ABLIKIM M, ACHASOV M N, AHMED S, et al[BESIII Collaboration]. Phys Rev D, 2019, 100(11): 111102. doi: 10.1103/PhysRevD.100.111102 [52] CHEN G Y, HUO W S, ZHAO Q. Chin Phys C, 2015, 39(9): 093101. doi: 10.1088/1674-1137/39/9/093101 [53] WANG Q, HANHART C, ZHAO Q. Phys Rev Lett, 2013, 111(13): 132003. doi: 10.1103/PhysRevLett.111.132003 [54] QIN W, XUE S R, ZHAO Q. Phys Rev D, 2016, 94(5): 054035. doi: 10.1103/PhysRevD.94.054035 [55] CLEVEN M, ZHAO Q. Phys Lett B, 2017, 768: 52. doi: 10.1016/j.physletb.2017.02.041 [56] CLEVEN M, WANG Q, GUO F K, et al. Phys Rev D, 2014, 90(7): 074039. doi: 10.1103/PhysRevD.90.074039 [57] ABLIKIM M, ACHASOV M N, ALBAYRAK O, et al[BESⅢ Collaboration]. Phys Rev Lett, 2013, 111(24): 242001. doi: 10.1103/PhysRevLett.111.242001 [58] WANG Q, HANHART C, ZHAO Q. Phys Lett B, 2013, 725(1-3): 106. doi: 10.1016/j.physletb.2013.06.049 [59] WANG Q, CLEVEN M, GUO F K, et al. Phys Rev D, 2014, 89(3): 034001. doi: 10.1103/PhysRevD.89.034001 [60] WU X G, HANHART C, WANG Q, et al. Phys Rev D, 2014, 89(5): 054038. doi: 10.1103/PhysRevD.89.054038 [61] ABAZOV V M, ABBOTT B, ACHARYA B S, et al[D0 Collaboration]. Phys Rev D, 2018, 98(5): 052010. doi: 10.1103/PhysRevD.98.052010 [62] GUO F K, HANHART C, MEISSNER U G, et al. Phys Lett B, 2013, 725: 127. doi: 10.1016/j.physletb.2013.06.053 [63] ABLIKIM M, ACHASOV M N, AI X C, et al[BESⅢ Collaboration]. Phys Rev Lett, 2014, 112(9): 092001. doi: 10.1103/PhysRevLett.112.092001 [64] GUO F K. Phys Rev Lett, 2019, 122(20): 202002. doi: 10.1103/PhysRevLett.122.202002 -




 下载:
下载:






































































































































































































































































































































































































 甘公网安备 62010202000723号
甘公网安备 62010202000723号