-
自20世纪80年代以来,随着世界范围内核物理大科学装置的广泛建设与先进探测技术的蓬勃发展,核物理的研究版图从传统的稳定原子核扩展到远离稳定线的区域,形成了超重原子核、不稳定原子核等系列学科前沿,并取得重要突破,如新合成的113-118 号系列超重元素[1-6]、新奇的中子晕现象[7-19]、手征对称性[20-35]、新幻数结构[36-44] 等。随着原子核物理实验和理论研究的发展,极大拓展的核素版图不仅含有地球上稳定存在的近300种与实验合成的近3 000 种核素,也包括理论预言存在的其他数千种核素,大部分为不稳定原子核。这些重要进展一方面极大丰富了人类的原子核物理知识,同时也对理论和实验研究提出新的挑战和发展机遇。
20世纪中叶,Mayer[45]和Haxel等[46-47]在平均势场近似基础上,唯象地引入强自旋-轨道耦合势,成功解释了原子核的传统幻数结构
$ N, Z\!=\!2 $ ,$ 8 $ ,$ 20 $ ,$ 28 $ ,$ 50 $ ,$ 82 $ 与$N\!=\!126$ ,并指出强的自旋-轨道耦合是核力的重要成分。随后,人们基于对核力的微观认识,如核力的介子交换理论[48],结合密度泛函思想,发展提出系列原子核密度泛函理论,并在描述各种原子核结构现象中取得了巨大的成功[49]。近年来,虽然理论上原子核结构的第一性原理研究取得了巨大进展[49],但仍旧局限于少数较轻的原子核。与之对比,发展日益成熟的原子核密度泛函理论能够对核素图上大部分核素提供合理的定量描述。典型的代表包括:非相对论框架下基于零程Skyrme力发展建立的Skyrme-Hartree-Fock理论[50]、基于有限程Gogny力建立的Gogny-Hartree-Fock 理论[51],以及基于相对论框架的相对论密度泛函理论[又称为协变密度泛函理论(CDFT)][52]。作为CDFT的重要分支,人们基于核力的介子交换图像,结合不同层次的平均场近似,发展建立了相对论平均场(RMF)理论[52]与相对论Hartree-Fock(RHF)理论[53]。在RMF 理论中,人们仅考虑了核力介子交换图像中直接项即Hartree项的贡献。早期Walecka[52]提出含标量势和矢量势的可重整化相对论平均场,即
$ \sigma $ -$ \omega $ 模型,成功解释了核物质的饱和机制。在此基础上,针对核力的低能非微扰特性,人们通过考虑介子场的非线性自耦合或引入介子-核子耦合强度的密度依赖,恰当处理了核力的介质效应[54],极大地提高理论描述的精确度,解决了核物质不可压缩系数过大等问题[55-56]。在含介子场非线性自耦合的相对论平均场(NL-RMF)理论中,人们通过考虑标量$ \sigma $ -、矢量$ \omega $ -介子以及同位旋矢量-矢量$ \rho $ -介子的非线性自耦合,发展提出系列RMF有效拉氏量,如NL系列[57-60]、TM系列[56]、PK系列[61]以及零程点耦合近似的PC-PK1[62]等。在相对论Brueckner-Hartree-Fock方法计算[63] 的启发下,人们将介子-核子耦合常数视为核子密度的函数,建立了密度依赖的相对论平均场(DDRMF)理论,并提出系列RMF拉氏量,如TW99[64]、DD-ME1[65]、DD-ME2[66]和 PKDD[61]等,进一步改善了对核物质不可压缩性与对称能等的理论描述[67-69]。由于理论的协变性,RMF 理论能自然给出核力重要成分——强的自旋-轨道耦合,并自洽解释了核结构中赝自旋与自旋对称性的起源[17,70-72],并在原子核结构与反应、原子核新奇现象、核天体物理等应用研究中取得巨大成功[73-76]。尽管如此,由于Hartree近似的局限性,重要的介子自由度如
$ \pi $ -介子与$ \rho $ -介子张量耦合等无法在RMF理论中得以有效考虑,特别是对原子核结构有重要影响的张量力成分。事实上,由于标准RMF理论计算所给出的$ N,Z\!=\!58 $ 与$ 92 $ 赝壳结构,RMF 理论系统性高估了相应核区的原子核结合能[77]。最近,实验测量也排除了$ Z\!=\!92 $ 子壳结构的可能性[78]。实质上,这些问题与RMF理论中所忽略的交换项即Fock项的效应关系密切。几乎在RMF 理论发展同时,显式包含Fock项贡献的RHF理论[53]也取得了一些进展,并系统应用于原子核结构研究[79-80]。之后,在处理核力的介质效应方面,人们分别通过考虑$ \sigma $ -介子与标量场$ \bar\psi\psi $ 的非线性自耦合,提升了RHF理论的描述精度,但仍无法与标准RMF理论相比。这与Fock项所带来的理论复杂性和数值计算困难直接相关。结合介子-核子耦合强度的密度依赖性,密度依赖的相对论Hartree-Fock(DDRHF)理论[81-82]最终解决了这一问题。基于所提出的RHF有效拉氏量PKO
$ i $ ($ i\!=\!1,2,3 $ )[81, 83] 与PKA1[82],RHF理论在原子核结构性质的定量描述上取得了与RMF理论同样的成功。同时,基于DDRHF理论及其扩展的相对论Hartree-Fock-Bogoliubov(RHFB)理论[84]的研究表明,Fock 项的引入改善了对原子核壳结构演化[83, 85-86]、有效质量[81]、相对论对称性[54, 82, 87-88]、张量力[89]、自旋-同位旋激发[90-91]以及$ \beta $ -衰变[92-93]、原子核新幻数结构[94-96]与新奇现象[88, 96]等的自洽描述。值得指出的是,通过引入$ \rho $ -介子张量耦合,RHF拉氏量PKA1 成功消除了RMF理论计算中长期存在的赝壳结构$ N,Z\!=\!58 $ 与$ 92 $ [54, 82],并自洽解释了Ca同位素中新幻数结构$ N\!=\!32 $ 与$ 34 $ [95-97]。围绕原子核结构中的基本问题——原子核壳结构,本文在扼要介绍RHF理论的基础上,综述RHF理论对原子核壳结构相关的研究,包括自旋-轨道劈裂相关的新幻数
$ N\!=\!32,34 $ 及其演化[95,97],赝自旋对称性恢复的新机制[54],及其相关中子晕现象[88]与超重幻数结构形成[98,94]等。 -
基于核力的介子交换图像,原子核内核子-核子相互作用由介子场传递,包括同位旋标量和矢量介子。在相对论密度泛函理论即CDFT中,人们利用同位旋标量-标量
$ \sigma $ -介子描述核力的中长程吸引部分,而同位旋标量-矢量$ \omega $ -介子描述核力的短程排斥部分。此外,引入同位旋矢量-矢量$ \rho $ -介子、同位旋矢量-赝标量$ \pi $ -介子描述核力的同位旋特性,光子场$ A $ 描述质子之间的电磁相互作用。因此,作为理论的出发点,RHF有效拉氏量密度$ {\cal{L}} $ 含有核子场 含有核子场$ \psi $ ,同位旋标量$ \sigma $ -和$ \omega $ -介子场,同位旋矢量$ \pi $ -和$ \rho $ -介子,以及光子场$ A $ 等自由度。考虑介子-核子的标量耦合($ \sigma $ -S)、矢量耦合($ \omega $ -V,$ \rho $ -V与$ A $ -V)、张量耦合($ \rho $ -T)以及赝矢量耦合($ \pi $ -PV),拉格朗日量密度可表述为[80]$$ \begin{array}{l} {\cal {L}}\!=\!{\cal {L}}_0+{\cal {L}}_I, \end{array} $$ (1) 其中
$ {\cal {L}}_0 $ 代表自由核子与介子场拉氏量密度,$ {\cal {L}}_I $ 对应介子-核子耦合部分的拉氏量密度$$ \begin{split} {\cal{L}}_0\!=&\bar{\psi}({\rm i}\gamma_\mu\partial^{\mu}-{{M}})\psi + \dfrac{1}{2}\partial_\mu\sigma\partial^\mu\sigma - \dfrac{1}{2}m^2_\sigma\sigma^2+ \\& \dfrac{1}{2}m^2_\omega\omega_\mu\omega^\mu - \dfrac{1}{4}\Omega_{\mu\nu}\Omega^{\mu\nu} + \dfrac{1}{2}\partial_\mu{{\pi}}\cdot\partial^\mu{{\pi}} - \dfrac{1}{2}m^2_\pi{{\pi}}\cdot{{\pi}}+\\& \dfrac{1}{2}m^2_{\rho}{{\rho}}_\mu\cdot{{\rho}}^\mu - \dfrac{1}{4}{{R}}_{\mu\nu}\cdot{{R}}^{\mu\nu} - \dfrac{1}{4}F_{\mu\nu}F^{\mu\nu},\\[-13pt]\end{split} $$ (2) $$ \begin{split} {\cal{L}}_I\!=\!&\bar{\psi}\Big[-g_\sigma\sigma - g_\omega\gamma^\mu\omega_\mu + \dfrac{f_\pi}{m_\pi}\gamma_5\gamma^\mu{{\tau}}\cdot\partial_\mu{{\pi}} + \\ & g_\rho\gamma^\mu{{\tau}}\cdot{{\rho}}_\mu - \dfrac{f_\rho}{2M}\sigma^{\mu\nu}{{\tau}}\cdot\partial_\nu{{\rho}}_\mu + e\gamma^\mu\dfrac{1-\tau_3}{2}A_\mu\Big]\psi{\text{。}} \end{split} $$ (3) 在拉氏量密度中,
${{M}}$ 和$ m_\phi $ ($\phi\!=\!\sigma$ ,$ \omega $ ,$ \rho $ ,$ \pi $ )分别为核子和介子质量,$ g_\phi $ ($ \phi\!=\!\sigma $ -S,$ \omega $ -V,$ \rho $ -V)和$ f_{\phi'} $ ($ \phi'\!=\!\rho $ -T,$ \pi $ -PV)则为介子-核子耦合强度。在自由拉氏量密度$ {\cal {L}}_0 $ [即(2)式]中,矢量场张量为$$ \begin{array}{l} \varOmega^{\mu\nu}\equiv\partial^\mu\omega^\nu-\partial^\nu\omega^\mu, \end{array} $$ (4) $$ \begin{array}{l} {{R}}^{\mu\nu}\equiv\partial^\mu{{\rho}}^\nu-\partial^\nu{{\rho}}^\mu, \end{array} $$ (5) $$ \begin{array}{l} \;\;\;F^{\mu\nu}\equiv\partial^\mu A^\nu-\partial^\nu A^\mu {\text{。}} \end{array} $$ (6) 在这些以及后续的公式中,我们用黑斜体代表同位旋矢量,黑体表示空间矢量。
利用Legendre变换,并代入介子场和光子场方程,由拉格朗日量密度(1)可得到系统的哈密顿量为
$$ \begin{split} H\!=\!&\displaystyle\int {\rm d}^3x\bar{\psi}(x)\left[-{\rm i}\gamma\cdot\nabla+M\right]\psi(x)+\\& \dfrac{1}{2}\displaystyle\sum\limits_{\phi}\displaystyle\int \displaystyle\int {\rm d}^3x {\rm d}^4x^\prime\bar{\psi}(x) \bar{\psi}(x^\prime)\varGamma_\phi D_\phi \psi(x^\prime)\psi(x){\text{。}} \end{split} $$ (7) 其中
$ \phi $ 代表标量耦合$ \sigma $ -S,矢量耦合$ \omega $ -V、$ \rho $ -V与$ A $ -V,张量耦合$ \rho $ -T,矢量张量耦合($ \rho $ -VT),赝矢量耦合$ \pi $ -PV等耦合道,对应的相互作用顶角$ \varGamma_{\phi} $ 为$$ \begin{array}{l} \varGamma_{ {\sigma{\rm{-S}} }}\!=\!-\big[g_\sigma\big]_{x}\big[g_\sigma\big]_{x^\prime}, \end{array} $$ (8) $$ \begin{array}{l} \varGamma_{ {\omega{\rm{-V}} }}\!=\!+\big[g_\omega\gamma_\mu\big]_{x}\big[g_\omega\gamma^\mu\big]_{x^\prime}, \end{array} $$ (9) $$ \begin{array}{l} \varGamma_{ {\rho \rm{-V} }}\!=\!+\big[g_\rho\gamma_\mu{{\tau}}\big]_{x}\cdot\big[g_\rho\gamma^\mu{{\tau}}\big]_{x^\prime}, \end{array} $$ (10) $$ \begin{array}{l} \varGamma_{ {\rho-{\rm{T}} }}\!=\!+\dfrac{1}{4M^2}\big[f_\rho\sigma_{\mu\nu}{{\tau}}\partial^\nu\big]_{x}\cdot\big[f_\rho\sigma^{\mu\lambda}{{\tau}} \partial_\lambda\big]_{x^\prime}, \end{array} $$ (11) $$ \begin{split} \varGamma_{ {\rho \rm{-VT}}}\!=\!&+\dfrac{1}{2M}\big[f_\rho\sigma_{\mu\nu}{{\tau}}\partial^\mu\big]_{x}\cdot\big[g_\rho\gamma^\nu{{\tau}}\big]_{x^\prime}+\\& \dfrac{1}{2M}\big[f_\rho\sigma_{\mu\nu}{{\tau}}\partial^\mu\big]_{x^\prime}\cdot\big[g_\rho\gamma^\nu{{\tau}}\big]_x, \end{split} $$ (12) $$ \begin{array}{l} \varGamma_{ {\pi \rm{-PV}}}\!=\!-\dfrac{1}{m_\pi^2}\big[f_\pi{{\tau}}\gamma_5\gamma_\mu\partial^\mu\big]_{x}\cdot\big[f_\pi{{\tau}}\gamma_5\gamma_\nu\partial^\nu\big]_{x^\prime}, \end{array} $$ (13) $$ \begin{array}{l} \varGamma_{ { A \rm{-V} }}\!=\!+\dfrac{e^2}{4}\big[ \gamma_\mu(1-\tau_3)\big]_{x}\big[\gamma^\mu(1-\tau_3)\big]_{x^\prime}{\text{。}} \end{array} $$ (14) 哈密顿量中的传播子
$ D_\phi $ 一般可写为$$ \begin{array}{l} D_\phi(x,x^\prime)\!=\!-\displaystyle\int \dfrac{{\rm d}^4k}{(2\pi)^4}{\rm e}^{-{\rm i}k(x-x^\prime)}\dfrac{1}{k^2-m^2_\phi}, \end{array} $$ (15) 其中
$ k $ 代表相互作用转移的四动量,$ m_\phi $ 为参与相互作用的介子质量。若忽略延迟效应,即忽略介子场和光子场所携带动量的时间分量,介子场和光子场的传播子可分别约化为Yukawa形式和库仑形式:$$ \begin{array}{l} D_\phi\!=\!\dfrac{1}{4\pi}\dfrac{e^{-m_\phi\mid{{x}}-{{x^\prime}}\mid}}{\mid {{x}}-{{x^\prime}}\mid}, D_{A\rm{-V}}\!=\!\dfrac{1}{4\pi}\dfrac{1}{\mid{{x}}-{{x^\prime}}\mid}{\text{。}} \end{array} $$ (16) 在RMF理论中,忽略延迟效应并不产生实质性的影响,因为Hartree近似,转移动量
$ k $ 为零。但在RHF理论中,对于Fock项而言,转移动量并不为零,忽略延迟效应意味着忽略相互作用传播的时间。对于大质量的介子来说,延迟效应的影响很弱,但对于轻质量$ \pi $ -介子来说,这一近似仍旧不失为一个开放性的问题[49, 80]。 -
与平均场近似相自洽,人们在量子化核子场
$ \psi $ 时通常会引入无海近似,即忽略反核子场对密度和流的贡献。基于Dirac方程的解对应的完备正交空间,核子场算符$ \psi $ 可展开为$$ \begin{array}{l} \psi(x)\!=\!\displaystyle\sum\limits_{i}\psi_i({{x}}){\rm e}^{-{\rm i}\varepsilon_i t}c_i, \end{array} $$ (17) 其中
$ \varepsilon_i>0 $ ,$ c_i^\dagger $ 与$ c_i $ 为Dirac方程正能解所对应的产生消灭算符,$ \psi_i $ 为Dirac旋量波函数。同时,展开式中已经略去Dirac 方程解空间中负能量态的贡献,即无海近似。在此基础上,可进一步得到量子化形式的哈密顿量[80]与质量数为$ A $ 的原子核Hartree-Fock基态,$$ \begin{array}{l} \left|{\varPhi}\right> \equiv \prod\limits_{i = 1}^A c_i^\dagger \left|{-}\right>, \end{array} $$ (18) 其中
$ \left|{-}\right> $ 为裸真空。取哈密顿量相对Hartree-Fock基态$ \left|{\Phi}\right> $ 的期待值可得到原子核系统的能量泛函,即$$ \begin{array}{l} E\!=\!\langle\varPhi|H|\varPhi\rangle\!=\!E^{\rm{kin.}}+\displaystyle\sum\limits_{\phi}(E^D_\phi+E^E_\phi), \end{array} $$ (19) 其中
$ E^{\rm{kin.}} $ 、$ E_\phi^D $ 与$ E_\phi^E $ 分别为动能部分、势能部分的直接项和交换项,$ \phi $ 代表各介子/光子-核子耦合道$ {\sigma } $ -S、$ {\omega} $ -V、$ {\rho } $ -V、$ {\rho } $ -T、$ {\rho } $ -VT、$ {\pi } $ -PV与$ { A } $ -V。在RMF 理论中,人们只考虑势能部分中的直接项贡献,而在RHF理论中则同时考虑直接项与交换项的贡献[80-82, 84]。具体的理论公式细节参考文献[73, 80-82, 84]等。在平均场近似基础上,为实现对原子核结构的精确描述,还需合理处理核力的介质效应。这里我们通过引入介子-核子耦合强度的密度依赖性来唯像处理复杂的介质效应,即,
$$ \begin{array}{l} g_i(\rho_b)\!=\!g_i(0)e^{-a_i\xi}, \;\;\;\;\;g_i\!=\!g_\rho,f_\rho, f_\pi; \end{array} $$ (20) $$ \begin{array}{l} g_i(\rho_b)\!=\!g_i(\rho_0)f_i(\xi),\;\;\;\;\;g_i\!=\!g_\sigma, g_\omega, \end{array} $$ (21) 其中
$ \xi\!=\!\rho_b/\rho_0 $ ($ \rho_0 $ 为核物质饱和密度),$ \rho_b\!=\!\bar\psi\gamma_0\psi $ 为核子密度,函数$ f_i $ 形式如下,$$ \begin{array}{l} f_i(\xi)\!=\!a_i\dfrac{1+b_i(\xi+d_i)^2}{1+c_i(\xi+d_i)^2}{\text{。}} \end{array} $$ (22) 在同位旋矢量耦合道中,方程(20)中
$ a_\rho $ 、$ a_\pi $ 与$ a_T $ 分别为耦合常数$ g_\rho $ 、$ f_\pi $ 与$ f_\rho $ 的密度依赖参数。对于同位旋标量耦合道$ {\sigma } $ -S与$ {\omega } $ -V,方程(21)中共有8个密度依赖的参数,即$ a_i $ 、$ b_i $ 、$ c_i $ 与$ d_i $ ($ i = \sigma,\omega $ )。为此,人们通常引入约束条件$ f_i(1)\!=\!1 $ ,$ f^{\prime\prime}_i(0)\!=\!0 $ ,$f^{\prime\prime}_\sigma(1) \!=\! f^{\prime\prime}_\omega(1) \!=\! 1 $ 以减少自由参数。在标准的RMF理论中,
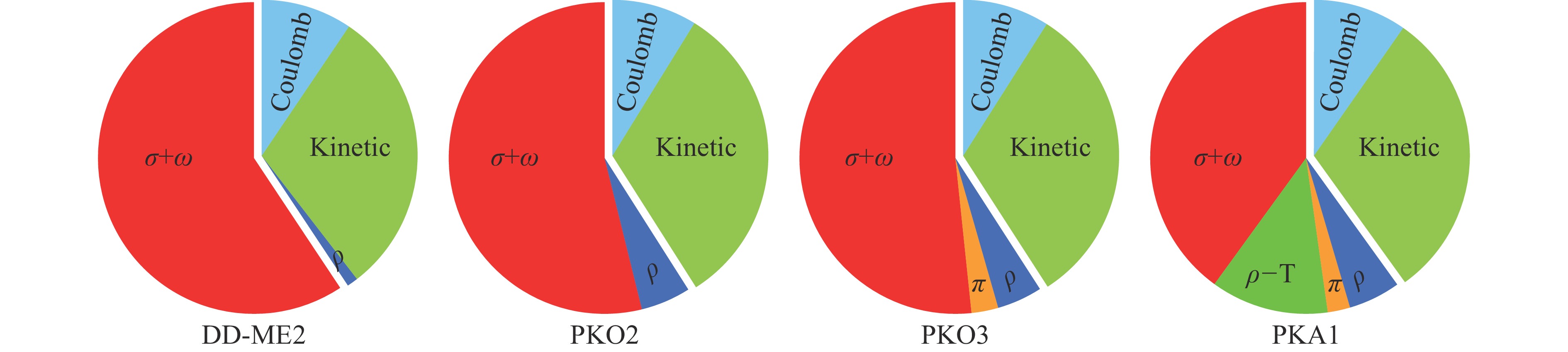
$ {\sigma } $ -S与$ {\omega } $ -V耦合分别描述核力中的强吸引与强排斥成分,而$ \rho $ -V耦合则描述核力的同位旋特性,$ { A } $ -V耦合描述电磁相互作用。在RHF理论中,由于Fock项的显式考虑,重要的系统自由度如$ {\pi } $ -PV与$ {\rho } $ -T(自然也引入$ {\rho } $ -VT)耦合得以自然考虑。因此,可以意料到Fock项将显著改变对核力各个成分的描述。正如文献[81]所指出的,Fock项的引入已经显著改变了$ {\sigma } $ -S与$ {\omega} $ -V所分别代表的强吸引与强排斥。在讨论Fock 项对原子核壳结构性质影响之前,有必要厘清Fock项对能量泛函的贡献。需要指出的是,基于核力的介子交换图像与平均场近似的思想,束缚的原子核基态是由核力中强吸引与强排斥平衡之后残余的吸引所决定,对应着原子核系统的动力学平衡。在CDFT 中,各耦合道对能量泛函的贡献则直接反映了理论上对原子核动力学平衡的建模情况。以208Pb为例,图1给出了动能项与各介子/光子-核子耦合道对能量泛函的贡献,其中凸出的扇形部分代表正(排斥)的贡献,其他则是负(吸引)的贡献。作为比较,图中展现了RMF有效拉氏量DD-ME2[66]与 RHF拉氏量PKO2[83]、PKO3[83]、PKA1[82]的计算结果。如图1所示,不同有效拉氏量给出的库仑场与动能项的贡献差别不明显,表明选定的有效拉氏量所给出的基态波函数近似一致。事实上,这也与不同模型给出近似一致的总能量泛函(结合能)相自洽[54]。然而,介子-核子耦合道对能量泛函的贡献则表现出显著的模型相关性。对于选定的有效拉氏量来说,同位旋标量道
$ \sigma $ -S和$ \omega $ -V之间的平衡$ \sigma+\omega $ ,即核力强吸引与强排斥之间的平衡保证了束缚的结合能(能量泛函)。从RMF有效拉氏量DD-ME2到RHF拉氏量PKO2,由于Fock项的贡献,同位旋矢量道$ \rho $ -V的贡献由排斥变为吸引。与之自洽,$ \sigma+\omega $ 的贡献在一定程度上被削弱。考虑$ {\pi } $ -PV的贡献后,即PKO3,强吸引与强排斥的平衡$ \sigma+\omega $ 被进一步微弱地削弱。而从PKO3到PKA1,由于$ {\rho } $ -T耦合引入的较强吸引势场,$ \sigma+\omega $ 的贡献被显著削弱,并从实质上改变了强吸引的$ \sigma $ -S和强排斥的$ \omega $ -V耦合之间的平衡。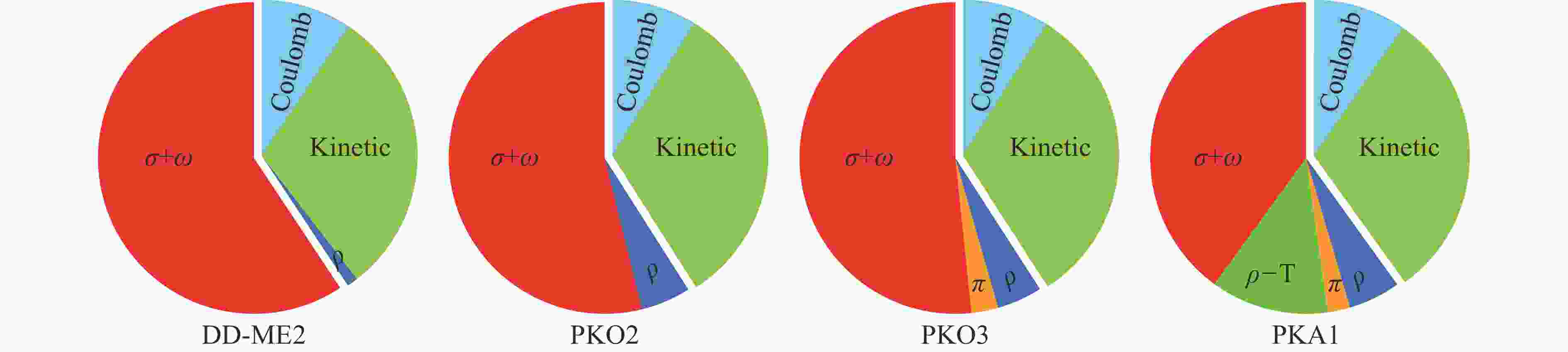
图 1 (在线彩图)有效拉氏量DD-ME2,PKO2,PKO3,PKA1的动能及各个介子-核子耦合道对208Pb能量泛函的贡献比例图。右侧凸出扇形代表正的(排斥的)贡献,而左侧代表负的(吸引的)部分,其中PKA1 的定量数据参考文献[54]中的表格1
正如后面将要详细讨论的,由于强的
${\rho{\rm{-T}} }$ 耦合效应,PKA1对原子核结构给出了实质上不同于其他CDFT的定量描述[54]。由图1,从RMF到RHF模型,Fock项的引入显著增强了同位旋矢量场,而实际上Fock 项对同位旋矢量相关的物理量如对称能等均有实质性的贡献[99-100]。另外,由图还可以看出$ {\pi \rm{-PV}} $ 耦合对能量泛函的贡献均比较弱,这是由于其耦合强度随密度增加呈指数衰减[81-83]。 -
近年来,随着放射性核束装置和探测技术的不断升级,原子核物理研究已从稳定核区往具有更加极端中质比的奇特核区不断扩展。随着中质比的变化,原子核的壳结构也会随之演化,进而涌现出不同于传统幻数结构的新子壳结构,如O同位素滴线附近
$ N = 16 $ 以及 Ca同位素丰中子核区的$ N\!=\!32 $ 与$ 34 $ 新幻数等[36-44]。为厘清原子核壳结构演化相关的物理机制,实验和理论不断地推进。沿着同位素链或同中子素链,随着中质比的变化,张量力由于其自旋相关的特性,在壳结构演化中扮演重要的角色[86, 89, 101]。基于核力的介子交换图像,RHF理论不仅保留了RMF理论自然给出强自旋-轨道耦合的优点,同时通过Fock项,也自然引入张量力成分的贡献,如$ {\pi \rm{-PV}} $ 与${\rho {\rm{-T}} }$ 耦合[89]。这也为在相对论的框架下探索丰中子原子核中新幻数结构的形成及其演化机制奠定了基础。 -
实验上,人们通过对丰中子Ca同位素
$ 2_1^+ $ 激发态能量的系统性研究[40-41]与精确的核质量测量[43]已证明在52Ca与54Ca中分别存在新的子壳结构$ N\!=\!32 $ 与34。为此,图2(a)与(b)分别给出了利用RHF拉氏量PKA1与RMF拉氏量DD-ME2计算得到的Ca同位素链正则单粒子能量$ \varepsilon^{\nu}_{nlj} $ 沿同位素链的演化。作为补充,图2(c)与(d)分别给出了RHF 拉氏量PKO3、PKA1与RMF拉氏量DD-ME2、DD-ME$ \delta $ [102]计算给出的中子($ \nu $ )平均对能隙$ \Delta^\nu $ 。从图中可以看出,RHF拉氏量PKA1再现了传统的幻数结构$ N\!=\!28 $ ,同时在$ N\!=\!32 $ 与34处给出显著的子壳结构。而RMF拉氏量 DD-ME2给出的单粒子能量随着中子数的增加近乎单调变化。与之相自洽,PKA1计算得到中子平均对能隙在$ N\!=\!28 $ 与32处为零,在$ N\!=\!34 $ 处$ \Delta^\nu $ 值也接近于零。而其他有效拉氏量计算得到的$ \Delta^\nu $ 值不支持在$ N\!=\!32 $ 与34处存在显著的壳结构。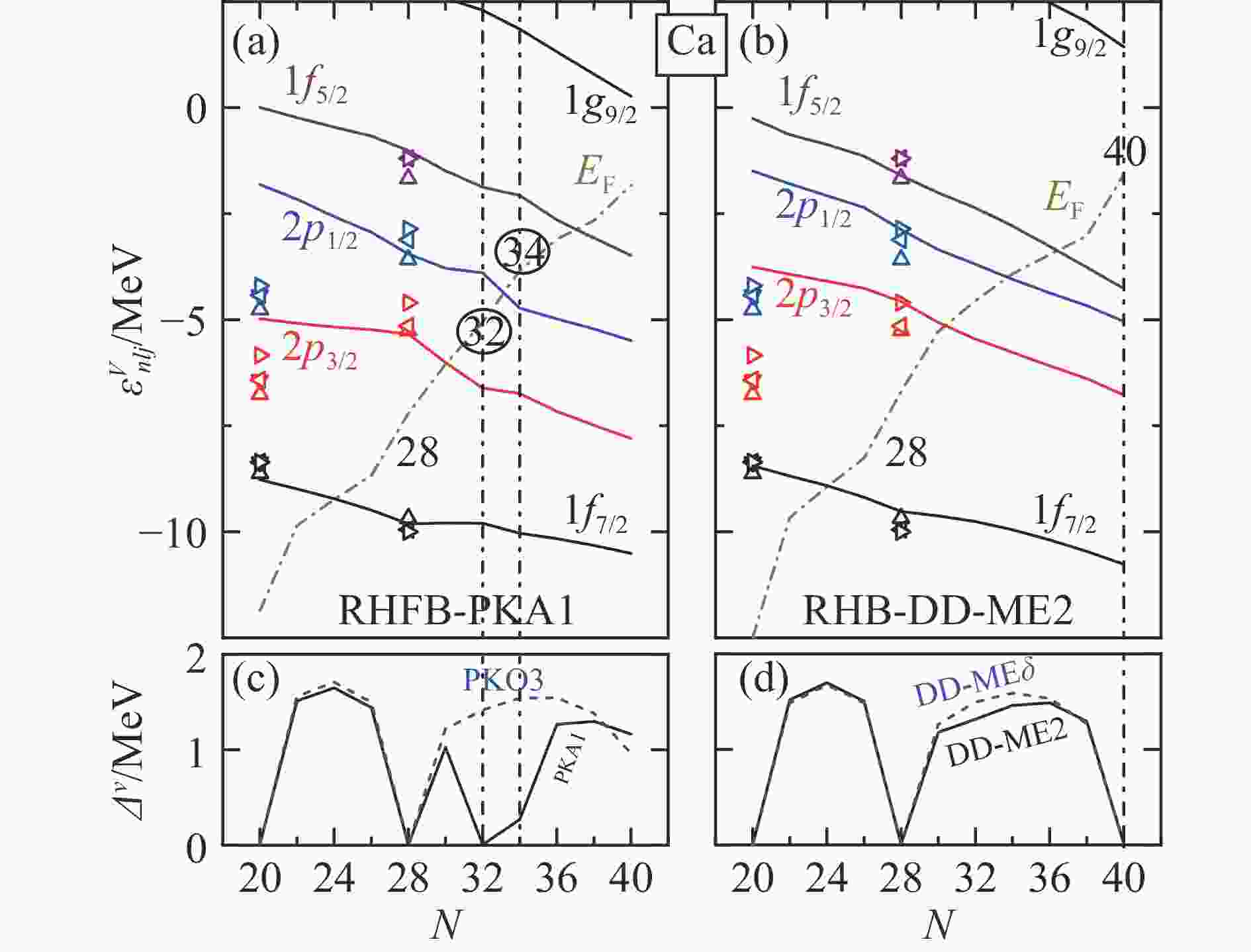
图 2 (在线彩图)RHFB/RHB理论计算的40-60Ca中子正则单粒子能级
$ \varepsilon^\nu_{nlj} $ 和平均对能隙$ \Delta^\nu $ ,图取自文献[95]为解释子壳结构
$ N\!=\!32 $ 与34的形成,图3(a)给出$ N\!=\!32 $ 子壳,即自旋轨道劈裂$ \Delta E_{\nu2p}(Z) $ 沿$ N\!=\!32 $ 同中子素链的演化,其中$ Z\!=\!20 $ (Ca)处的$ \Delta E_{\nu 2p} $ 值被选为参考基础。从Ni到Ca,随着质子数减少,PKA1 计算给出的中子$ \nu2p $ 轨道劈裂相比其他有效拉氏量显著增大,最终给出52Ca中亚壳结构$ N\!=\!32 $ 。随着质子数进一步减少,即从Ca到S,PKA1给出的$ \Delta E_{\nu2p} $ 值虽稍有降低,结合图2(a)可以看出$ N\!=\!32 $ 子壳结构在50Ar 与48S中仍旧十分显著,这与最新的实验结果[103]和理论研究[97]一致。为理解图3(a)中显著的模型差异,图3(b)展现了PKA1中$ \pi $ -PV和$ \rho $ -T 耦合道对$ \Delta E_{\nu2p} $ 值的贡献。与图3(a)相比,同位旋矢量$ \pi $ -PV和$ \rho $ -T耦合的贡献几乎完整解释了PKA1与PKO3之间的差别。同时也可看出,相比$ \pi $ -PV和$ \rho $ -T耦合中的张量力成分,中心力成分的贡献更为重要,两者均显著增强了中子$ \nu2p $ 轨道的劈裂。而随着质子数进一步减少,由于张量力和中心力贡献相互抵消,$ \pi $ -PV和$ \rho $ -T耦合的效应基本可以忽略。 -
虽然从同中子素演化的角度,文献[95]通过分析同位旋矢量
$ \pi $ -PV和$ \rho $ -T耦合效应成功解释了$ N\!=\!32 $ 子壳结构的形成。然而,沿$ N\!=\!34 $ 同中子素链的演化研究表明,$ \pi $ -PV和$ \rho $ -T耦合效应无法解释$ N\!=\!34 $ 子壳结构的形成。这主要是由于张量力和中心力成分的贡献相互抵消。因此,在文献[95]中利用RHF有效拉氏量PKA1虽然成功再现了新子壳结构$ N\!=\!32 $ 与$ 34 $ ,并从同中子素演化的角度揭示了$ N\!=\!32 $ 子壳结构的形成机制,但并未阐明$ N\!=\!34 $ 子壳的形成机制。针对这一点,文献[97]结合最近丰中子核55-57Ca质量的精确测量[43],利用RHF有效拉氏量PKA1、PKO3以及RMF拉氏量DD-ME2,通过分析沿Ca 同位素链的壳结构演化,给出新子壳结构$ N\!=\!32 $ 与$ 34 $ 形成机制的统一自洽解释。图4(a)展现了PKA1,PKO3和DD-ME2计算得到的双中子分离能
$ S_{2n} $ 沿Ca同位素链的演化,并与最新的实验结果[43]比较。从$ N\!=\!28 $ 到$ 30 $ ,实验双中子分离能$ S_{2n} $ 急剧减小,对应传统中子幻数结构$ N\!=\!28 $ ,所选定的拉氏量均能很好地再现这一结果。类似地,作为子壳结构$ N\!=\!32 $ 与$ 34 $ 存在的直接证据,$ S_{2n} $ 值从$ N\!=\!32 $ 到$ N\!=\!36 $ 持续显著降低。在选定的有效拉氏量中,PKA1很好地再现了$ N\!=\!30 $ 到32处的平台以及从$ N\!=\!32 $ 到36持续显著降低的趋势,而 PKO3与DD-ME2则给出自$ N\!=\!30 $ 处开始平缓下降的趋势,并在$ N\geqslant35 $ 处呈现平台结构。作为直观的子壳结构定量信息,图4(b)与(c)分别给出了经验壳隙$\delta_e\!=\!S_{2n}(N) - S_{2n}(N+1)$ 和双中子壳隙$ \Delta_{2n}\!=\!S_{2n}(N) - S_{2n}(N+2) $ 。图中结果表明,三组有效拉氏量均能很好再现传统的$ N\!=\!28 $ 壳结构信息,但对于新子壳结构$ N\!=\!32 $ 与$ 34 $ ,PKO3和DD-ME2明显低估了壳隙的大小,而PKA1则很好地再现了实验数据。为更好地理解52Ca与54Ca中子壳结构
$N\!=\!32$ 与$ 34 $ 的形成机制,图5给出52,54Ca的核子密度分布(a)与中子单粒子能级(b)示意图。从图中可以看,52Ca呈现出中心凸起的中子和质子密度分布,而54Ca 的中子密度分布中心区域被显著压低,呈现类气泡结构,质子中心密度相比52Ca也被显著压低。根据文献[96, 104-106]中所指出的核物质密度分布与自旋-轨道劈裂之间的自洽关系,即中心凸起(压低)的密度对应较大(较小)的低轨道角动量态(如$ p $ 态)自旋-轨道劈裂,不难理解图5中52Ca中显著的中子$ \nu2p $ 轨道劈裂在54Ca 中明显变小。相比之下,中子$ \nu 1f $ 轨道劈裂从52Ca到54Ca则近乎不变,这是因为随着轨道角动量增加,显著增强的离心位垒将驱使核子远离中心区域,因此中心区域密度的变化对高角动量态自旋-轨道劈裂的影响很小。因此从52Ca到 54Ca,$ \nu2p $ 轨道劈裂显著减少和$ \nu1f $ 轨道劈裂近乎不变,两者促使54Ca中子壳结构$ N\!=\!34 $ 的形成。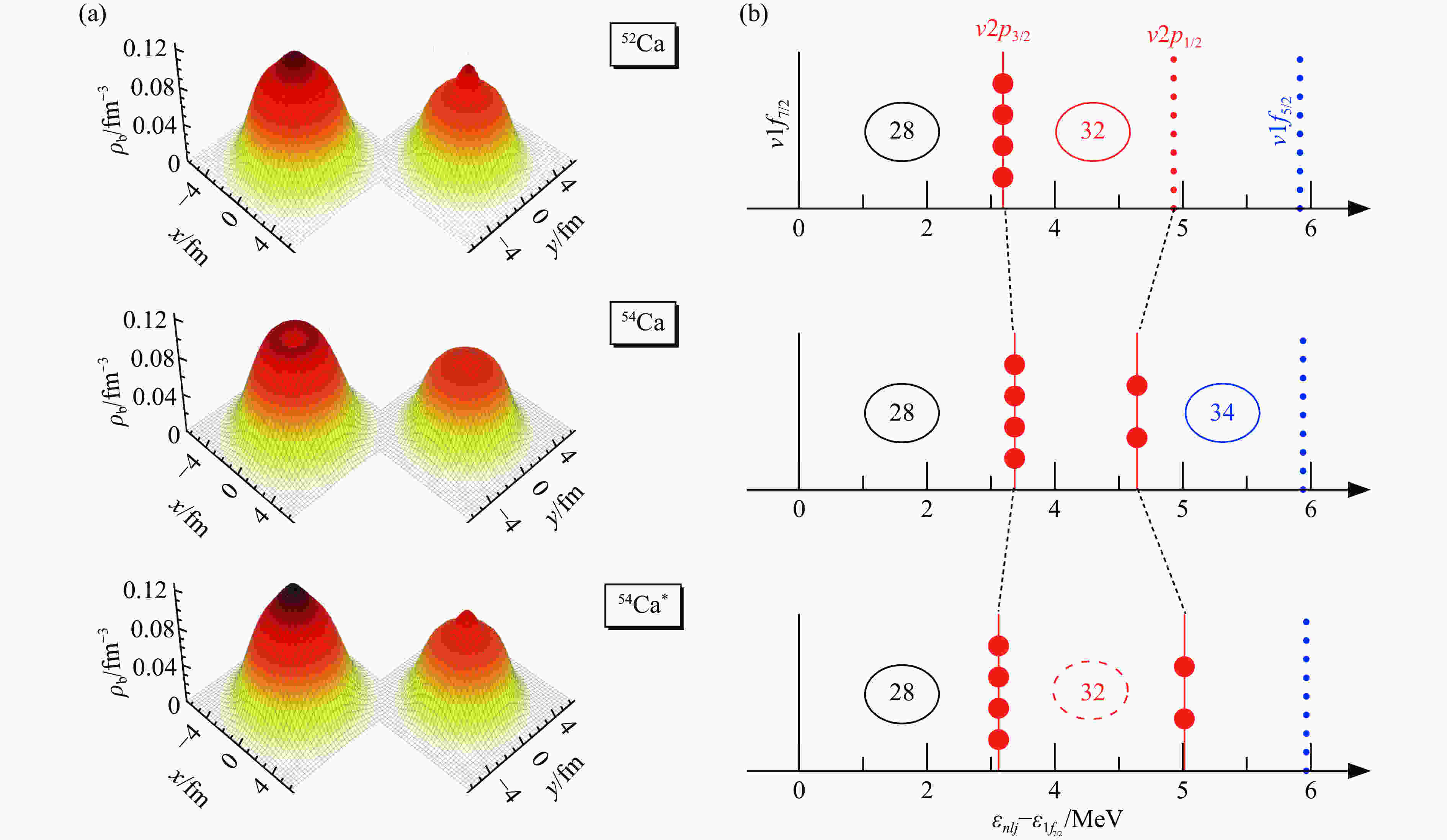
图 5 (在线彩图)52,54Ca中子/质子密度分布(a)与中子单粒子能级(相对于
$ \nu1f_{7/2} $ 轨道)$E_{nlj}\!=\!\varepsilon_{nlj} - \varepsilon_{1f_{7/2}}$ (b)值得注意的是,原子核中心区域密度分布显著压低或者(类)气泡结构的形成通常是因为费米面附近
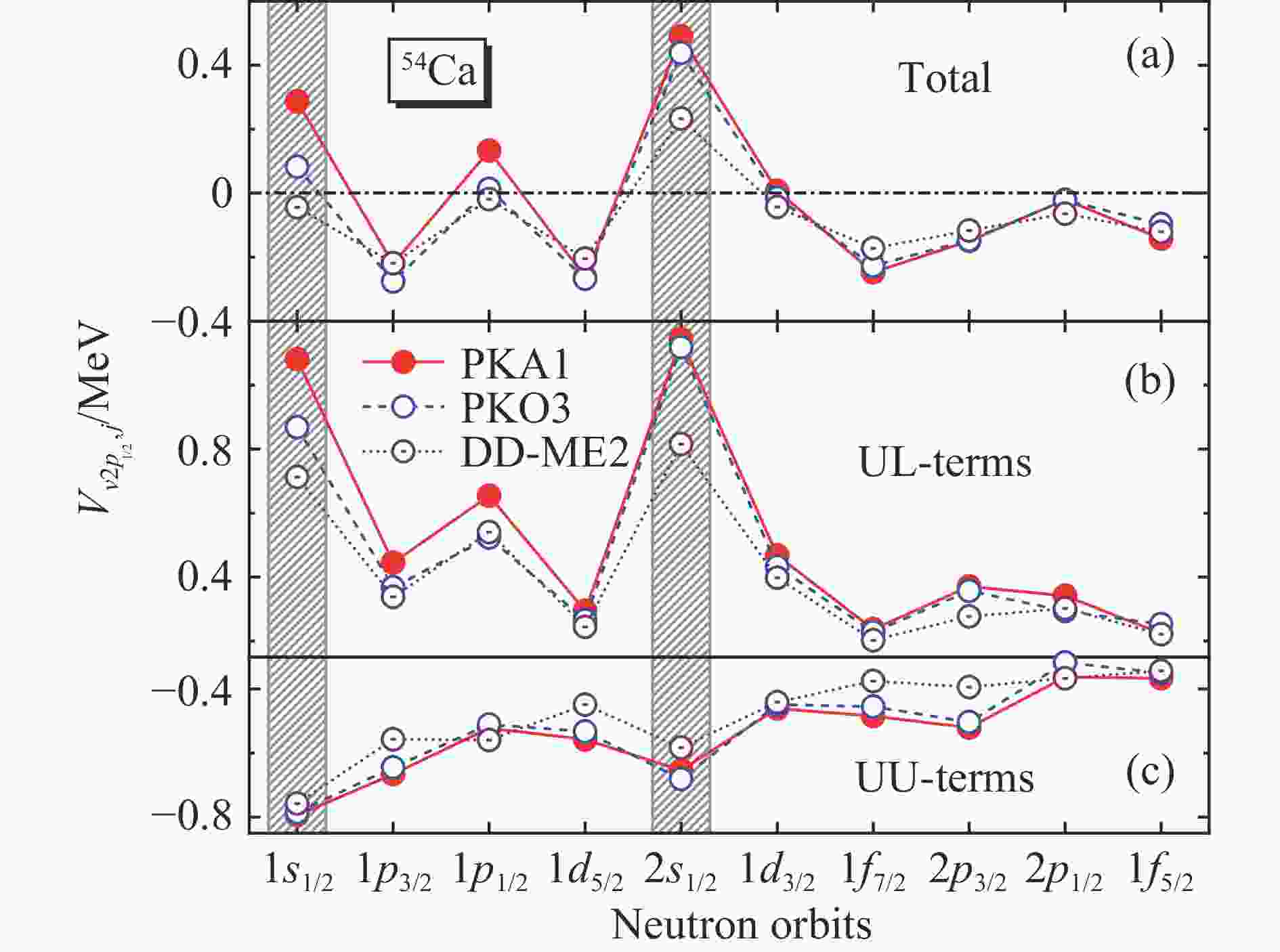
$ s_{1/2} $ 轨道未占据,如质子类气泡核34Si[107-108]。而从52Ca到54Ca,中子和质子$ s_{1/2} $ 轨道的占据数并没有改变,增加的两个价中子占据$ \nu2p_{1/2} $ 轨道。为解释从52Ca到54Ca中心区域核子密度分布的显著变化,图6(a)给出价中子$ \nu $ 2p$ _{1/2} $ 轨道与中子轨道的相互作用矩阵元。从图中可以看出,$ \nu2p_{1/2} $ 与$ \nu s_{1/2} $ 轨道之间呈现强的排斥相互作用。这意味着从52Ca到54Ca,价中子占据$ \nu2p_{1/2} $ 轨道,$ \nu2p_{1/2} $ 与$ \nu s_{1/2} $ 轨道之间的排斥效应将驱使$ \nu s_{1/2} $ 轨道上的中子远离中心,由此形成类气泡结构。同时,由于中子-质子相互作用,占据$ \pi s_{1/2} $ 轨道的质子($ \pi $ )也随之远离中心区域,从而显著压低了54Ca中心区域的质子密度分布。在相对论框架下,
$ p_{1/2} $ 态的Dirac旋量上分量(下分量)与$ s_{1/2} $ 态的下分量(上分量)具有相同的轨道量子数。我们称具备这种特性的两个量子态为狄拉克反转伴态(Dirac inversion partners,DIPs)。因此,我们将图6(a) 中所示相互作用矩阵元分解为UL-项和UU-项,即分别为图6(b)与(c)。其中,UU-项仅包含Dirac旋量上分量的贡献,而剩余部分为UL-项,主要由 Dirac旋量上下分量之间的耦合贡献。一般而言,对于正能量态,由于下分量对核子密度的贡献极小,相互作用矩阵元主要由UU-项决定。然而从图6(b)来看,UL-项都表现为排斥作用,并且DIPs 之间的反转相似性进一步增强了这种排斥效应,从而导致排斥的DIPs相互作用。事实上,排斥的UL-项主要由同位旋标量道($ \sigma $ -S和$ \omega $ -V)决定,因此这一排斥效应与模型无关[97]。此外,从RMF有效拉氏量DD-ME2到RHF 的PKO3与PKA1,由于矢量耦合($ {\omega } $ -V和$ {\rho } $ -V)空间分量Fock项的贡献,排斥的UL-项进一步增强。需要特别指出的是,从PKO3到PKA1,DIPs$ \nu1s_{1/2} $ 与$ \nu2p_{1/2} $ 之间的排斥效应也显著增强,这是因为PKA1给出了不同于PKO3 的核力吸引与排斥平衡[54]。为检验DIPs之间的排斥效应在从52Ca到54Ca密度和壳结构演化中的作用,我们采用PKA1,在54Ca自洽迭代计算中扣除中子
$ s $ -轨道受到的来自于其DIP$ \nu2p_{1/2} $ 轨道排斥的UL-项,相应计算结果见图5的第三行,标记为54Ca*。显然,扣除价中子轨道$ \nu2p_{1/2} $ 对$ \nu s_{1/2} $ 排斥的UL-项后,中子和质子密度分布呈现出类似于52Ca的中心凸起结构,并给出显著的$ \nu2p $ 轨道劈裂,人为消除了亚壳$ N\!=\!34 $ 。这表明了DIPs$ \nu2p_{1/2} $ 与$ \nu s_{1/2} $ 之间强的排斥效应对$ N\!=\!34 $ 亚壳的形成十分关键。对于
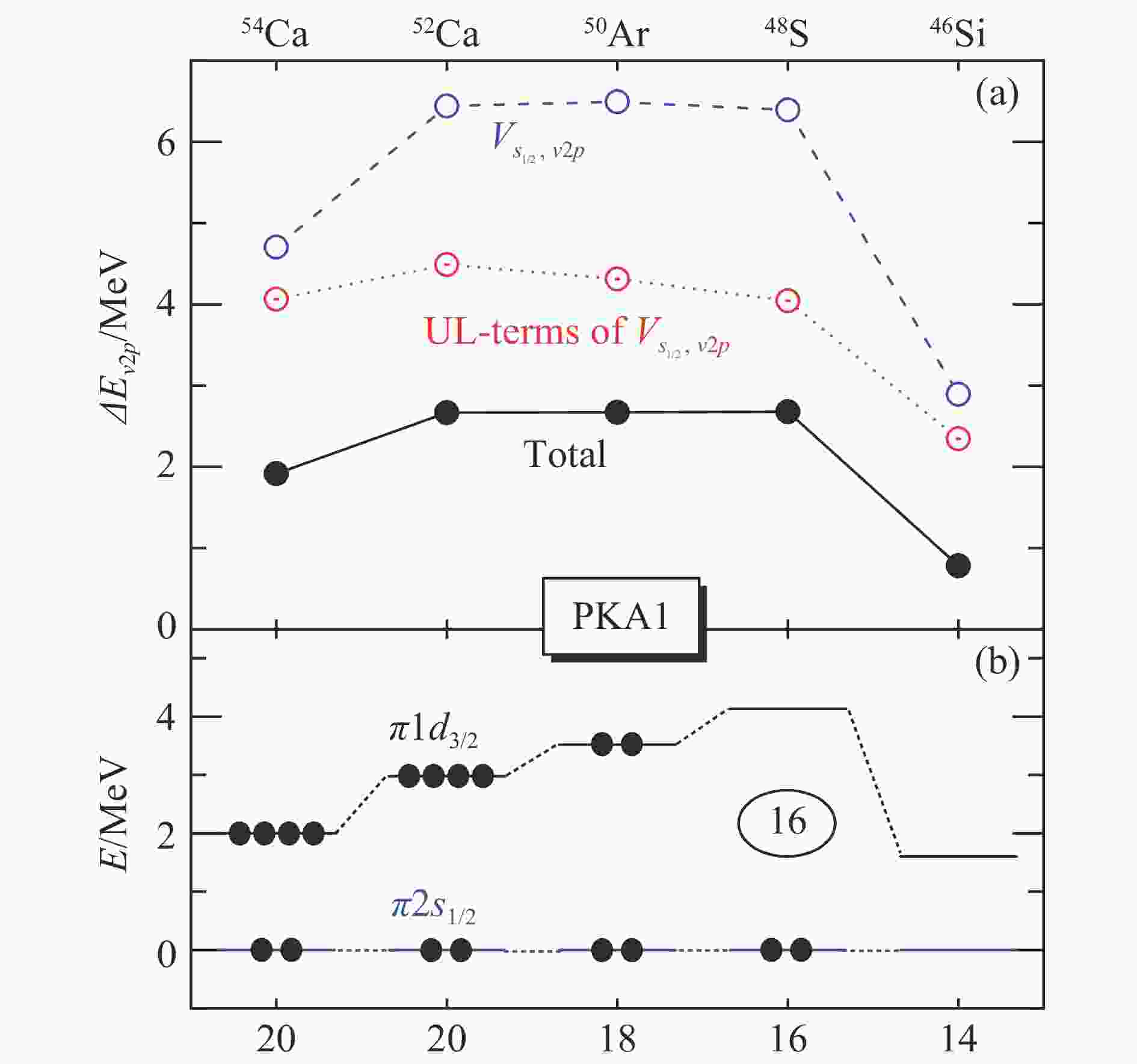
$N\!=\!32$ 亚壳从Ni到Ca的演化,图3表明$ \pi $ -PV和$ \rho $ -T耦合效应十分重要。随着质子数进一步减少,子壳结构$N\!=\!32$ 依然显著。事实上,实验上已经确认51K与50Ar中的$N\!=\!32$ 子壳结构[103, 109]。针对这一问题,图7(a)给出从54Ca到52Ca以及进一步沿$N\!=\!32$ 同中子素链到46Si中子$ \nu2p $ 轨道劈裂$ \Delta E_{\nu2p} $ 的演化,图7(b) 则展现了相应质子价轨道的演化。沿$ N\!=\!32 $ 同中子素链,从52Ca到48S$ \nu2p $ 轨道劈裂(实心圆圈)基本不变,而从48S到46Si,$ \Delta E_{\nu2p} $ 值急剧减小,即46Si中亚壳$ N\!=\!32 $ 消失。因此,48S为缺质子侧最后一个保留$ N\!=\!32 $ 亚壳结构的偶偶核。为解释
$ N\!=\!32 $ 亚壳结构的演化,图7(a)中同时给出了$ s_{1/2} $ 轨道对$ \nu2p $ 轨道劈裂的贡献及其UL-项贡献。结果表明,$ \nu2p_{1/2} $ 轨道的DIP,即$ s_{1/2} $ 轨道的贡献,特别是其UL-项几乎完整地解释了$ N = 32 $ 亚壳结构的演化。从 48S到46Si,$ \pi2s_{1/2} $ 轨道不再被质子占据,相应的$ s $ -轨道贡献也显著降低,进而导致46Si中$ N\!=\!32 $ 亚壳结构的消失。与之不同的是,从52Ca到54Ca,$ s $ -轨道贡献的变化由于价中子轨道$ \nu2p_{1/2} $ 的占据,DIPs 之间的排斥效应使得$ s $ -轨道中心区域的几率密度显著压低,进而削弱了$ \nu2p $ 轨道劈裂。尽管如此,这两者均根源于DIPs ($ s_{1/2},p_{1/2} $ )之间由于反转相似性导致的强耦合效应。从中也可以看出,新幻数结构$ N\!=\!32 $ 与$ 34 $ 的形成均源于DIPs 之间的强耦合。需要指出的是,原子核中出现幻数壳结构不仅体现在质量的系统变化上,如这里关注的双中子分离能(如图4),也会体现在半径系统变化上,如Pb同位素电荷半径的同位旋漂移[110]。然而,对Ca同位素中新的子壳结构
$ N\!=\!32 $ 与$ 34 $ ,有研究表明52,54Ca的电荷半径异常增大[111-112],这在一定程度上挑战了我们对幻数结构形成的传统认识。从文献[97]所揭示的子壳结构$ N\!=\!32 $ 与$ 34 $ 形成机制来看,52,54Ca中价轨道的占据几率并没有发生异常的变化。同时,由于中子DIPs之间的强排斥,$ s $ -轨道的几率密度分布在一定程度上变得更加弥散,这势必会增大原子核的半径包括电荷半径。事实上,理论自洽计算给出的52,54Ca 电荷半径符合已有的实验观测[112]。 -
类似于自旋对称性的破缺在原子核壳结构及其演化中的重要地位,原子核赝自旋对称性的提出很好地解释了实验上观测到的原子核形变与超形变带、全同带等[113-116]。1997年,Ginocchio[70-71]指出赝自旋对称性是一种相对论对称性,而所谓赝轨道角动量
$ \tilde{l} $ 即狄拉克旋量的下分量角动量$ l^{\prime} $ 。在相对论框架下,若用$ n, l, j $ 分别表示主量子数、狄拉克旋量上分量角动量、总角动量,则赝自旋伙伴态($n, l, j\!=\!l+1/2$ )和($n-1, l+2, j\!=\!l+3/2$ )可重新标记为($\tilde{n}\!=\!n-1, \tilde{l}\!=\!l+1\!=\!l^{\prime}, \tilde{j}\!=\!l^\prime\pm1/2$ )。同时,赝自旋对称性守恒条件被证明为标量势$ S(r) $ 与矢量势$ V(r) $ 之和为零,即$V(r)+ S(r)\!=\!0$ [70],其中$ r $ 为径向距离。该条件可被一般化为${\rm d}[V(r)+S(r)]/ {\rm d}r\!=\!0$ [117]。需要指出的是,赝自旋对称性守恒条件$V(r)+S(r)\!=\!0$ 或${\rm d}[V(r)+S(r)]/ {\rm d}r\!=\!0$ 对应着原子核中核力强吸引与强排斥之间的某种平衡。 -
如图1,与其他有效拉氏量相比,PKA1中同位旋标量
$ {\sigma} $ -S与$ {\omega } $ -V耦合之间的平衡明显不同,这是由于${\rho {\rm{-T}} }$ 耦合贡献的较强吸引。这一改变与赝自旋对称性守恒条件$V(r)+S(r)\!=\!0$ 或${\rm{d}}[V(r)+S(r)]/{\rm{d}}r\!=\!0$ 关系密切。事实上,PKA1 消除了标准RMF理论计算中普遍存在的赝壳结构$ N,Z\!=\!58 $ 和$ Z\!=\!92 $ ,而这些赝壳对应着高角动量态的赝自旋对称性破缺。以幻数核48Ca、90Zr、132Sn、208Pb以及理论预言的超重幻数核310120[94]为代表,图8(b)给出费米面附近的质子赝自旋-轨道(PSO)劈裂$ \Delta E_{\rm{PSO}} $ (MeV)。显然,仅PKA1很好地再现了实验参考数据,而其他有效拉氏量均系统地高估了$ \Delta E_{\rm{PSO}} $ 值。对比图8(a) 所示质子壳,208Pb中高估的$ \Delta E_{\rm{PSO}} $ 值对应着明显低估的幻数壳$ Z\!=\!82 $ 。类似的在中重核区,子壳结构$ Z\!=\!64 $ 的形成也与赝自旋对称性的恢复密切相关。由于赝自旋伙伴态$ (\pi2d_{5/2},\pi1g_{7/2}) $ 相关的赝自旋对称性恢复,即赝壳$ Z\!=\!58 $ 的消除,PKA1成功再现了子壳结构$ Z\!=\!64 $ 及其同位旋演化[85]。在超重核区,赝自旋对称性的恢复/破缺和超重幻数结构的形成关系密切,如质子$ Z\!=\!120 $ 、$ 126 $ 与中子$ N\!=\!184 $ 壳结构[94]。
图 8 (在线彩图)实验及协变密度泛函理论给出的(a)质子壳隙(MeV)和(b)费米面附近的质子赝自旋-轨道(PSO)劈裂
$ \Delta E_{\rm{PSO}} $ (MeV)。具体细节见正文,图取自文献[54]以208Pb为例,图8(a)给出质子PSO劈裂
$ \Delta E_{\rm{PSO}}^\pi $ (MeV)随赝轨道角动量$ l' $ 的演化,包括从深束缚到费米面附近的赝自旋伙伴态;图(b)则给出了动能项、$ {\sigma{\rm{-S}} } $ 与$ {\omega{\rm{-V}} } $ 耦合对$ \Delta E_{\rm{PSO}}^\pi $ 的贡献,即$ E_{\rm{kin.}+\sigma+\omega} $ 项。对比图9(a)中PKA1、PKO3与DD-ME2的结果,可以发现PKA1计算的$ \Delta E_{\rm{PSO}}^\pi $ 值呈现强的角动量依赖性,最终在费米面附近恢复了赝自旋对称性,很好再现了实验参考结果。结合图9(b),可以发现$ \Delta E_{\rm{PSO}}^\pi $ 值相对于赝轨道$ l' $ 的系统性主要取决于同位旋标量$ {\sigma{\rm{-S}} } $ 与$ {\omega{\rm{-V}} } $ 耦合的贡献$ E_{\rm{kin.}+\sigma+\omega} $ 项。不同于PKA1,PKO3和DD-ME2给出的$ \Delta E_{\rm{PSO}}^\pi $ 值均呈现弱的角动量依赖性,包括其$ E_{\rm{kin.}+\sigma+\omega} $ 项。
图 9 (在线彩图)PKA1、PKO3与DD-ME2计算得到的(a)208Pb质子赝自旋-轨道劈裂
$ \Delta $ E$ ^\pi_{PSO} $ 随赝轨道角动量$ l^\prime $ 的演化,(b)同位旋标量$ {\sigma{\rm{-S}} } $ 与$ {\omega\rm{-V} } $ 耦合以及动能项对$ \Delta $ E$ ^\pi_{\rm{PSO}} $ 的贡献。$ 1.0\kappa_\rho $ 和$ 0.0\kappa_{\rho} $ 标记着基于PKA1实验性有效拉氏量,具体细节见正文。图取自文献[54]为了理解模型之间的差异,图10给出选定拉氏量同位旋标量[图10(a)]和同位旋矢量[图10(b-c)]耦合强度的密度依赖行为。结合图1所示能量泛函,从DD-ME2到PKO3随着Fock 项的引入,同位旋矢量的贡献由排斥变为吸引并显著增强。与之相洽,同位旋标量
$ {\sigma{\rm{-S}} } $ 和$ {\omega{\rm{-V}} } $ 耦合强度和密度依赖性均显著降低,即图10(a)。尽管如此,无论DD-ME2还是PKO3,同位旋标量耦合强度$ g_\sigma $ 和$ g_\omega $ 的密度依赖行为近乎平行。事实上,这一现象在DDRMF有效拉氏量中普遍存在。而对于PKA1,$ \rho $ -T耦合贡献了较强的吸引,显著改变了$ {\sigma{\rm{-S}} } $ 和$ {\omega{\rm{-V}} } $ 之间的平衡及其对能量泛函的贡献,见图1。由图10(c) 可见,$ \kappa_{\rho} $ 强的密度依赖性表明$ \rho $ -T耦合也对介质效应有实质性的贡献。因此相比PKO3,PKA1中$ g_\sigma $ 与$ g_\omega $ 的密度依赖性显著降低,密度依赖行为也不再平行,$ g_\sigma $ 值也有显著降低。事实上,这与图1能量泛函的变化自洽[54]。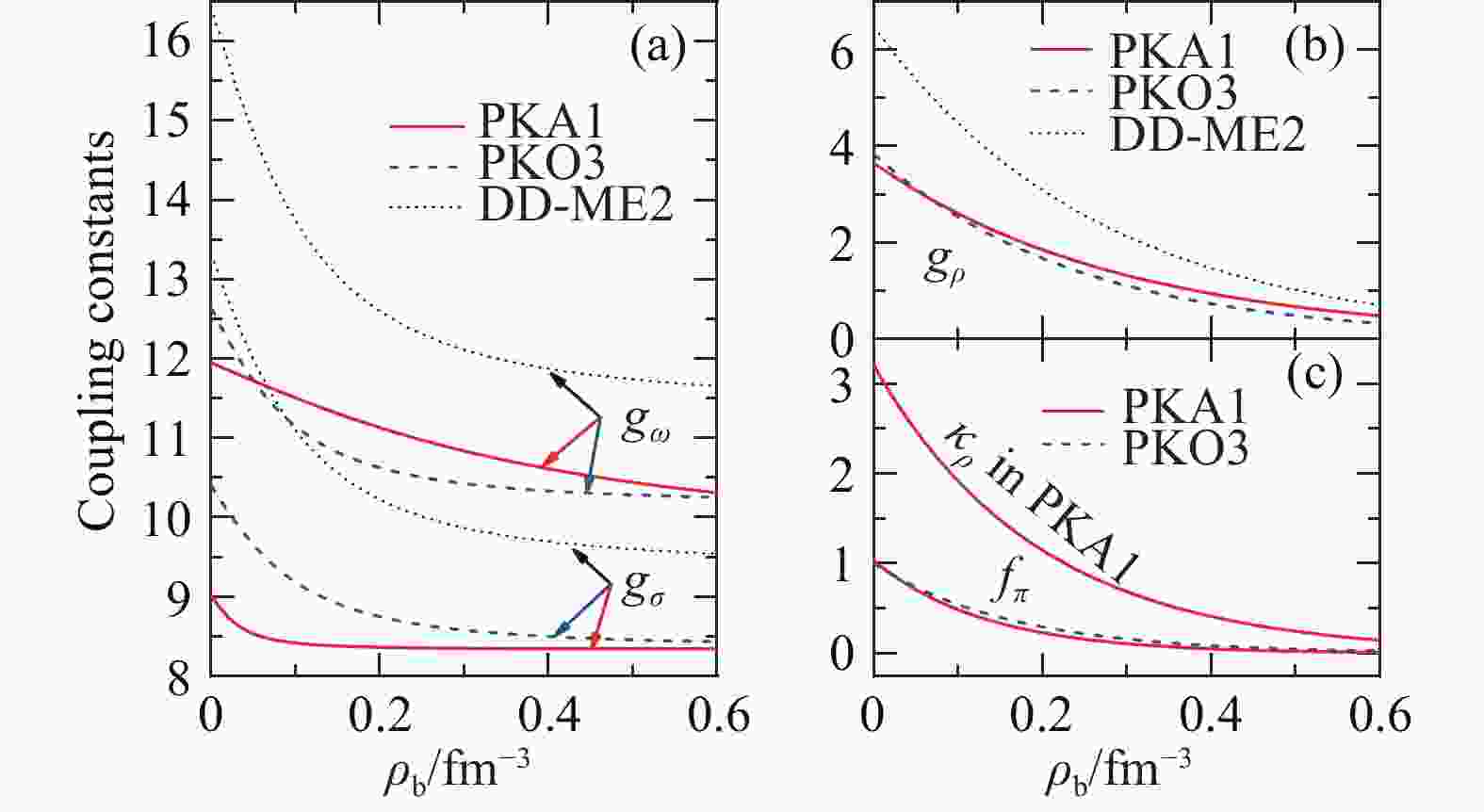
图 10 (在线彩图)有效拉氏量PKA1、PKO3与DD-ME2中耦合强度(a)
$ g_\sigma $ 与$ g_\omega $ 、(b)$ g_\rho $ ,以及(c)$\kappa_\rho\!=\!f_\rho/g_\rho(0)$ 与$ f_\pi $ 随密度$ \rho_b $ (fm–3) 的变化。图取自文献[54]为了探索采用介子-核子耦合强度密度依赖性所模拟的介质效应对赝自旋对称性恢复的影响,我们从PKA1出发,首先将
$ g_\omega $ 的密度依赖行为取为与$ g_\sigma $ 一致,同步调整$ g_\sigma(0) $ 与$ g_\omega(0) $ 的值保证所得到的208Pb 结合能不变,并把所得到的有效拉氏量标记为$ 1.0\,\kappa_\rho $ 。在此基础上,关闭$\rho$ -T耦合,并同步调整$ g_\sigma(0) $ 与$ g_\omega(0) $ 的值保证所得到的208Pb结合能不变,所得拉氏量记为$ 0.0\,\kappa_\rho $ 。利用$ 1.0\,\kappa_\rho $ 与$ 0.0\,\kappa_\rho $ 计算所得到赝自旋轨道劈裂结果如图9所示。拉氏量$ 1.0\,\kappa_\rho $ 与$ 0.0\,\kappa_{\rho} $ 的计算结果均表明,同位旋标量$ {\sigma } $ -S与$ {\omega } $ -V耦合强度,即$ g_\sigma $ 与$ g_\omega $ 平行的密度依赖行为导致赝自旋劈裂弱的角动量依赖性。而类似于从PKO3到DD-ME2的变化,从$ 1.0\,\kappa_\rho $ 到$ 0.0\,\kappa_\rho $ ,由于削弱的同位旋矢量耦合贡献,同位旋标量耦合$ {\sigma } $ -S与$ {\omega } $ -V之间平衡对$ \Delta E_{\rm{PSO}}^\pi $ 的贡献系统性增强,如图9(b)所示。综合而言,代表核力强吸引与强排斥的同位旋标量耦合$ {\sigma} $ -S与$ {\omega } $ -V之间平衡,及其所携带的核力介质效应对高角动量态赝自旋对称性的恢复十分重要,其中$ {\rho } $ -T耦合扮演了重要的角色[54]。事实上,结合原子核中核子的几率密度分布与角动量之间的关系,不难理解核介质中核力吸引-排斥平衡对赝自旋轨道劈裂角动量依赖性的影响。随着核子角动量的增加,由于离心位垒的排斥使得核子几率分布从中心区域逐渐外移到原子核表面,同时原子核密度也从饱和密度附近下降到零密度。在RHF拉氏量PKA1中,由于
$ g_\sigma $ 与$ g_\omega $ 的密度依赖行为不再平行,核力强吸引$ {\sigma} $ -S与强排斥$ {\omega } $ -V之间的平衡随核子密度的变化显著,这一变化表现为赝自旋轨道劈裂$ \Delta E_{\rm{PSO}}^\pi $ 强的角动量依赖性。从赝自旋对称性恢复角度,这一特征也为约束核力的介质效应提供定性的参考性指导。 -
如图8所示,壳结构的形成与附近赝自旋对称性的恢复关系密切。事实上这也与文献[118]所揭示自旋-轨道耦合和赝自旋轨道劈裂之间关系自洽,因为壳结构如
$ Z\!=\!50 $ 与$ 82 $ 源于强的自旋-轨道耦合效应。类似的在$ N\!=\!82 $ 同中子素中,如146Gd,子壳$ Z\!=\!64 $ 既可视为源于$ \pi2d $ -轨道的劈裂,同时也可发现子壳上下各有一组近似简并的赝自旋伙伴态[85]。在超重原子核区,由于能级密度的增加,类似的现象更为普遍。基于RHFB理论的自洽计算,文献[94]预言208Pb之后的超重质子幻数为
$ Z\!=\!120 $ 、中子幻数为$ N\!=\!184 $ 。图11给出了预言的超重双幻核304120的质子(a)与中子(b) 单粒子能谱,计算采用的有效拉氏量包括RMF的PKDD与DD-ME2、RHF的PKO$ i $ ($ i\!=\!1,2,3 $ )与PKA1。从图中可以看出,所选的有效拉氏量均给出壳结构$ Z\!=\!120 $ [94, 98],这一结果与基于非相对论Skyrme-Hartree-Fock理论的 SLy6,SkI1,SkI3和SkI4等计算一致。需要注意的是,该壳结构由赝自旋伙伴态$ (\pi3p_{3/2},\pi2f_{5/2}) $ 之间的显著劈裂给出。而对于$ N\!=\!184 $ ,PKA1给出最为显著的中子壳结构,并在壳的上下各有一对近似简并的赝自旋伙伴态,即$ (\nu2h_{11/2},\nu1j_{13/2}) $ 与$ (\nu4s_{1/2},\nu3d_{3/2}) $ 。相比之下,对于赝自旋伙伴态$(\nu2h_{11/2}, \nu1j_{13/2})$ ,其他有效拉氏量均给出显著劈裂,即中子壳$ N\!=\!198 $ ,相应的中子壳$ N\!=\!184 $ 被明显压制。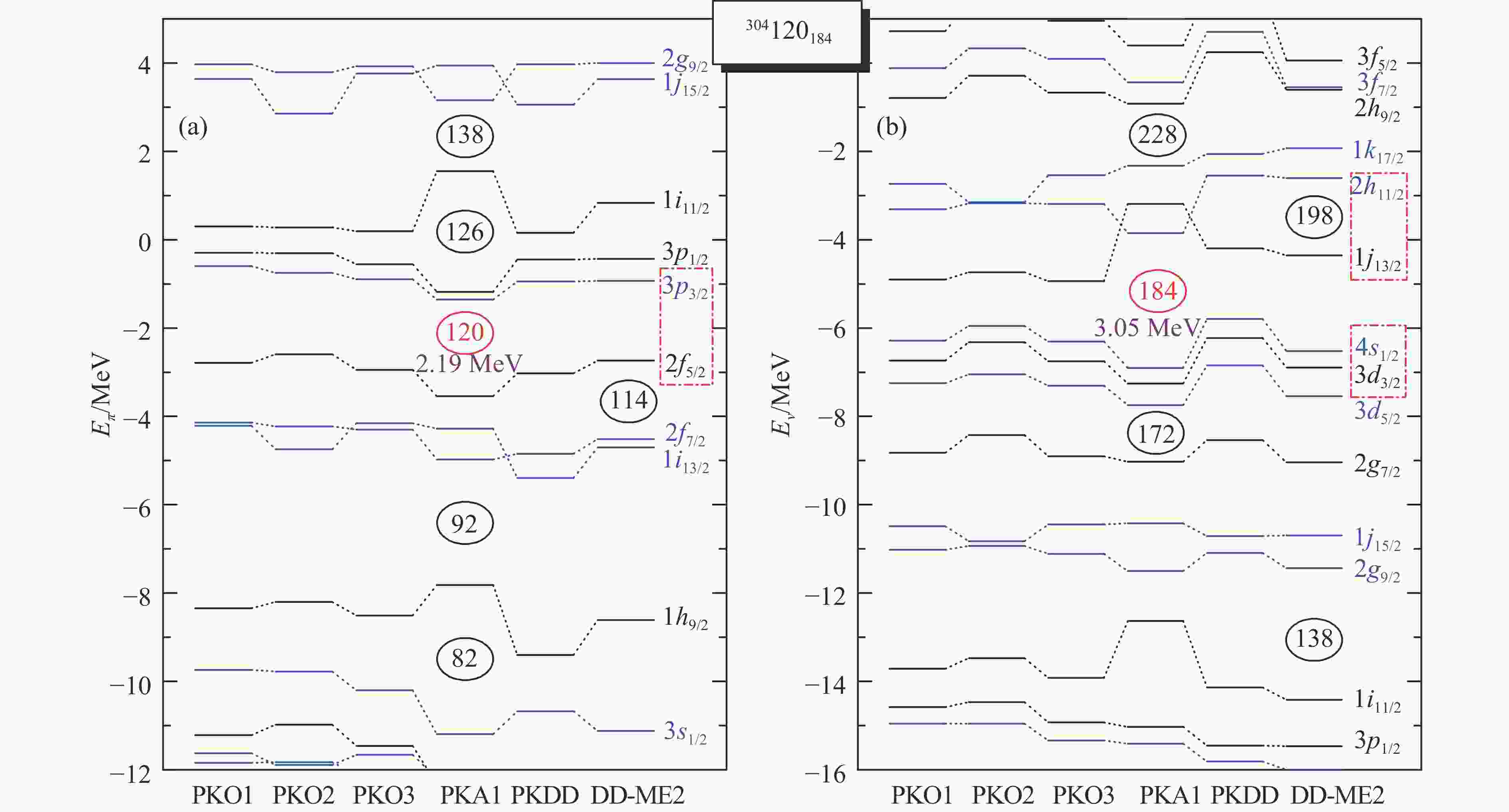
图 11 (在线彩图)超重核304120质子(a)和中子(b)单粒子能谱,采用的有效拉氏量包括RMF的PKDD与DD-ME2、RHF的PKO
$ i $ ($i\!=\!1,2,3$ )与PKA1。图取自文献[94]为理解超重核304120中壳结构
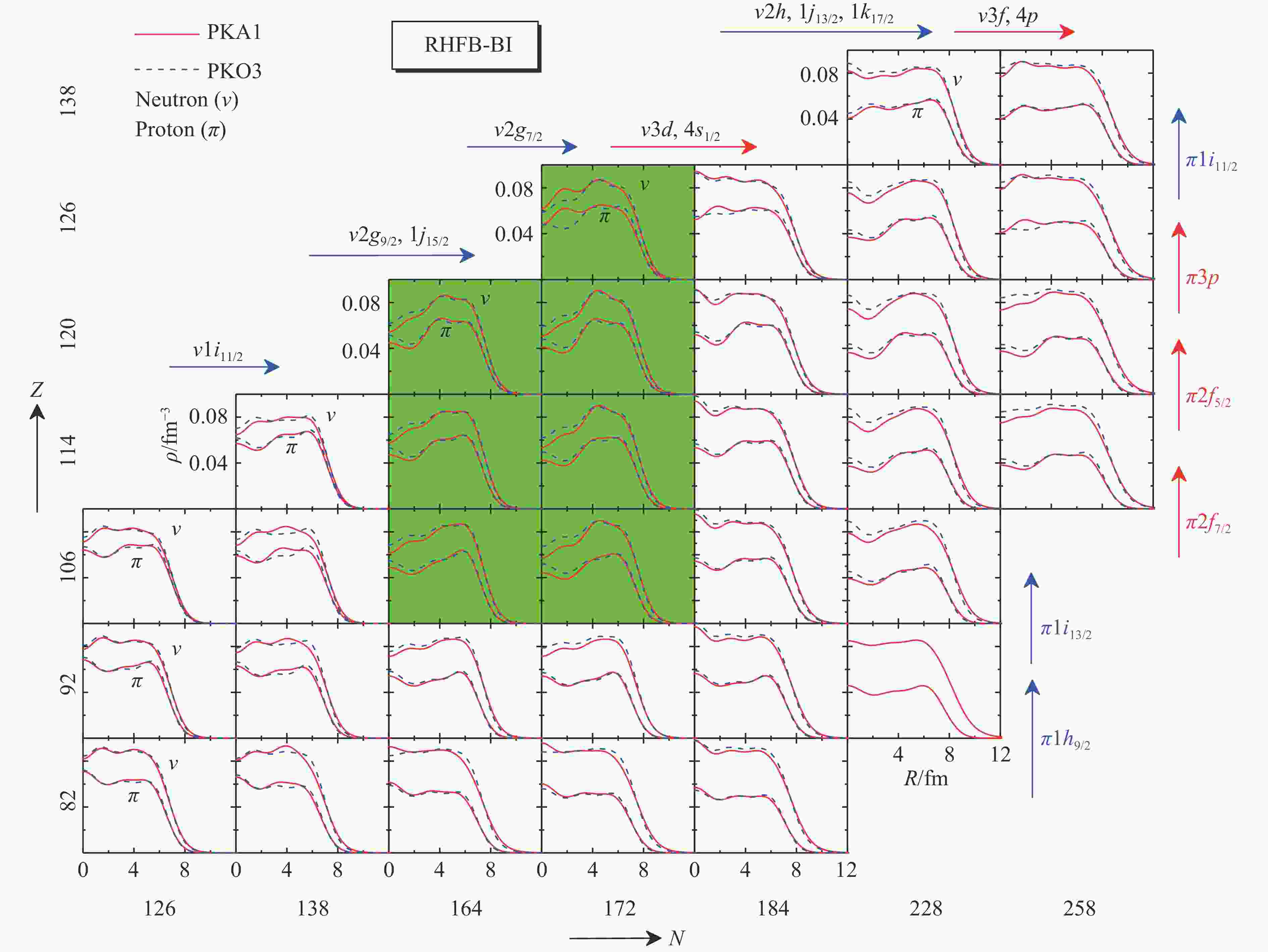
$ Z\!=\!120 $ 、$ N\!=\!184 $ 与赝自旋对称性恢复/破缺之间的关系,图12给出了208Pb之后代表性重核与超重核的中子与质子密度分布图,其中结果由采用有效拉氏量PKA1与PKO3的RHFB理论计算给出,对力为有限程 Gogny对力D1S[119]。随着中子数和质子数的增加,中子和质子均占据高角动量的单粒子态,如中子的$ \nu1i_{11/2} $ 、$ \nu2g_{9/2} $ 、$ \nu1j_{15/2} $ 和质子的$ \pi1h_{9/2} $ 、$ \pi1i_{13/2} $ 等。由于显著的离心位垒和持续增强的库仑排斥,原子核靠近表面区域的密度被显著抬升,从而形成典型的类气泡结构,即中心区域相比峰值区域被显著压低。根据中心区域密度分布与低角动量态自旋-轨道劈裂以及赝自旋轨道劈裂之间的自洽关系,不难理解图11中小的$ \pi3p $ -轨道劈裂与显著的赝自旋伙伴态$ (\pi3p_{3/2},\pi2f_{5/2}) $ 劈裂,进而形成质子$ Z\!=\!120 $ 壳。对于中子来说,由于强的离心位垒,高角动量的赝自旋伙伴态$ (\nu2h_{11/2},\nu1j_{13/2}) $ 劈裂受中心区域密度分布的影响很小,而低角动量的$ (\nu4s_{1/2},\nu3d_{3/2}) $ 则是因为节点效应的缘故,类气泡结构的影响也被显著削弱。因此,中子$ N\!=\!184 $ 壳附近的赝自旋对称性恢复较好,促使壳结构$ N\!=\!184 $ 的形成。不同于轻核区48Si[96]与54Ca[97]等中子类气泡结构的形成,超重核区中心区域密度分布的压低与显著增强的库仑排斥、离心位垒以及
$ s $ -态不被占据等密切相关。在一定程度上,超重核中类气泡结构的形成类似轻核34Si[107]与48Si[96]等中质子类气泡结构的形成,但密度被压低的区域比轻核区要大得多,更多的态包括$ d $ 、$ f $ 态也受到显著的影响,如与质子壳$ Z\!=\!120 $ 相关$ \pi2f_{5/2} $ 轨道。因此相比稳定核区来说,影响超重核区幻数结构形成的机制更为复杂。赝自旋对称性的恢复/破缺不仅与超重幻数结构的形成关系密切,同时也会影响到奇特原子核中新奇现象,如巨晕结构的形成。基于RHFB理论模型,文献[88]PKA1预言在
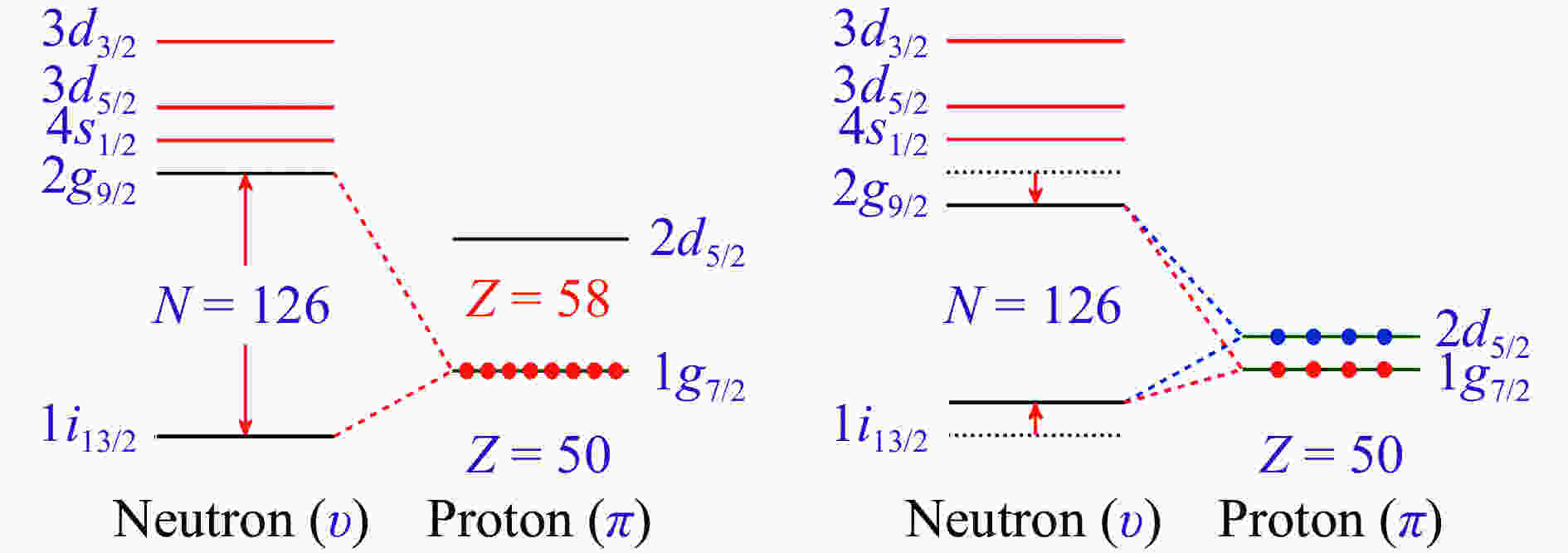
$ 58 $ 号元素铈(Ce) 的中子滴线附近存在中子巨晕结构,对应的中子滴线为$ N\!=\!140 $ ,而其他RMF与RHF有效拉氏量PKO$ i $ 则预言Ce的中子滴线为$ N\!=\!126 $ 。研究表明,这一模型差异与质子赝自旋伙伴态$ (\pi2d_{5/2},\pi1g_{7/2}) $ 的劈裂密切相关。如图13左侧所示,在RMF理论与RHF的PKO$ i $ 计算中,质子赝自旋伙伴态$ (\pi2d_{5/2},\pi1g_{7/2}) $ 劈裂显著,形成赝壳结构$ Z\!=\!58 $ 。因此,Ce同位素中的价质子完全占据$ \pi1g_{7/2} $ 轨道。基于RHFB理论的自洽计算[88] 表明,由于节点效应,$ \pi1g_{7/2} $ 与中子$ \nu1i_{13/2} $ 态的耦合明显强于和$ \nu2g_{9/2} $ 态的耦合,从而导致明显的$ N\!=\!126 $ 中子壳。然而,在PKA1的计算中,如图13右侧所示,由于赝自旋对称性的恢复,赝壳结构消失,价质子也大量占据$ \pi2d_{5/2} $ 轨道。不同于$ \pi1g_{7/2} $ 轨道,$ (\pi2d_{5/2},\nu2g_{9/2}) $ 耦合与$(\pi2d_{5/2}, \nu1i_{13/2})$ 耦合差别并不显著[88]。因此,与左侧相比,中子壳$N\!=\!126$ 被显著削弱,从而中子滴线得以进一步外推,壳上方的低角动量$ s $ 与$ d $ 态被中子占据,促使晕结构的形成。近期,结合Dirac Woods-Saxon基展开[120],成功发展了轴对称形变的相对论Hartree-Fock理论,并初步应用于轻质量原子核结构性质的研究[121]。研究发现,包含
$ \pi $ -PV耦合的RHF有效拉氏量PKO3和PKO1 系统改善了对形变核20Ne性质的描述。同时,由于张量力所特有的自旋相关性,$ \pi $ -PV 耦合在决定原子核单粒子能级结构随形状演化中扮演了重要角色。因此,对于核素图上大部分形变原子核来说,尤其是不稳定原子核以及超重原子核,有必要基于新发展的轴对称形变的相对论Hartree-Fock理论,系统探索$ \pi $ -PV和$ \rho $ -T 耦合中自然引入的张量力成分[89, 122] 对原子核结构特性的影响。 -
本文综述了相对论Hartree-Fock(RHF)理论对原子核壳结构性质的近期相关研究,包括丰中子原子核中新子壳结构
$ N\!=\!32 $ 与$ 34 $ 的形成机制、高角动量态的赝自旋对称性恢复新机制及其与超重幻数结构、原子核巨晕现象的自洽关系等,并着重关注了RHF 理论所引入的Fock项对原子核结构的影响。针对Ca同位素中新子壳结构
$ N\!=\!32 $ 与$ 34 $ ,基于RHF理论的研究表明:(1) 沿同中子素链的演化中,$ {\rho } $ -T与$ {\pi } $ -PV耦合效应成功解释了$ N\!=\!32 $ 子壳结构从Ni到Ca的系统性增强,其中张量力成分也提供了实质性的贡献,但无法解释$ N\!=\!34 $ 子壳结构的系统性增强;(2) 沿Ca同位素链的演化中,子壳结构$ N\!=\!32 $ 与$ 34 $ 的形成分别源于中子$ \nu2p $ 轨道劈裂在52Ca中的显著增强和54Ca中的显著削弱,相应地,中心核子密度分布从52Ca的中心凸起演变为54Ca 的中心凹陷或平缓结构;(3) 狄拉克伴态[Dirac inversion partners (DIPs)]之间的强耦合是影响中子$ \nu2p $ 轨道劈裂演化的关键机制,由此给出子壳结构$ N\!=\!32 $ 与$ 34 $ 形成的统一自洽解释。赝自旋对称性是原子核结构中的一种相对论对称性。随着原子核质量数的增加,核子能级密度逐渐增加,因此结合赝自旋对称性恢复/破缺的研究,对理解重核中的壳结构性质具有十分重要的参考价值。以双幻重核208Pb 为例,基于协变密度泛函理论的研究发现,赝自旋轨道劈裂的角动量相关性由核介质中代表强吸引的标量耦合与代表强排斥的矢量耦合之间的平衡直接决定,可视为核介质中核力吸引-排斥平衡的结构性体现。这不仅揭示了Fock项包括
$ {\rho } $ -T耦合等的重要效应,同时为约束核力介质效应的理论描述提供了定性参考。此外,结合赝自旋对称性的恢复/破缺,论文还综述了超重原子核中幻数结构以及丰中子原子核中新奇巨中子晕现象的形成机制,为理解相关物理现象提供了独特视角。
-
摘要: 一直以来,原子核壳结构是原子核物理研究的重点关注内容。特别是随着近年来新一代放射性核束装置和探测技术的蓬勃发展,丰中子原子核中新的壳结构及其演化与形成机制等成为核物理关注的热点之一。在基于核力介子交换图像建立的相对论Hartree-Fock 理论框架下,本工作以Ca同位素、双幻核 208Pb、超重核以及极端丰中子核为例,综述丰中子原子核中新的壳结构形成机制,高角动量态赝自旋对称性恢复与介质中核力吸引-排斥平衡,赝自旋对称性恢复/破缺与原子核壳结构、新奇现象等研究工作,并着重关注了与原子核新壳结构形成、赝自旋对称性恢复以及新奇现象等密切相关的交换(Fock)项效应。
-
关键词:
- 新幻数结构 /
- 赝自旋对称性 /
- 超重核 /
- 奇特核 /
- 相对论Hartree-Fock
Abstract: For a long time, nuclear shell structure is an important issue of nuclear physics. In particular, with rapid development of new generation of nuclear radioactive ion beam facilities and detectors, new shell structures appearing in neutron-rich nuclei have largely attracted the interests of the field, including the mechanism behind and the evolutions. Under the frame of relativistic Hartree-Fock theory founded on the meson-exchange diagram of nuclear force, taking calcium isotopes, doubly magic nuclide 208Pb and the selected superheavy and exotic nuclei as examples, this paper reviews the occurrence of new sub-shells in neutron-rich nuclei, the pseudo-spin symmetry (PSS) restoration and the in-medium nuclear attraction-repulsion balance, the PSS restoration/violation and nuclear shell structure, novel phenomena, etc., in which the roles of the Fock terms are intensively discussed. -
图 1 (在线彩图)有效拉氏量DD-ME2,PKO2,PKO3,PKA1的动能及各个介子-核子耦合道对208Pb能量泛函的贡献比例图。右侧凸出扇形代表正的(排斥的)贡献,而左侧代表负的(吸引的)部分,其中PKA1 的定量数据参考文献[54]中的表格1
图 2 (在线彩图)RHFB/RHB理论计算的40-60Ca中子正则单粒子能级
$ \varepsilon^\nu_{nlj} $ 和平均对能隙$ \Delta^\nu $ ,图取自文献[95]图 3 (在线彩图)中子
$ \nu2p $ 轨道劈裂随$N\!=\!32$ 同中子素链演化图(a) 四组有效拉氏量PKA1、PKO3、DD-ME2和DD-ME$ \delta $分别给出的中子$ \nu2p $轨道劈裂$ \Delta E_{\nu2p}(Z)- \Delta E_{\nu2p}(20) $沿$N\!=\!32$同中子素链的演化;(b) PKA1 有效拉氏量中各成分对壳演化的贡献。图取自文献[95]
图 5 (在线彩图)52,54Ca中子/质子密度分布(a)与中子单粒子能级(相对于
$ \nu1f_{7/2} $ 轨道)$E_{nlj}\!=\!\varepsilon_{nlj} - \varepsilon_{1f_{7/2}}$ (b)注:第三行54Ca*代表扣除中子$ \nu2p_{1/2} $轨道对$ s_{1/2} $轨道UL-项贡献的54Ca自洽计算结果。具体细节见正文,图取自文献[97]。
图 7 (在线彩图)同中子素链
$N\!=\!32$ 和54Ca中的中子$ \nu2p $ 态自旋轨道劈裂$ \Delta {\rm{E}}_{\nu2p} $ (a) 中子$ \nu 2p $态总的自旋轨道劈裂(黑色实心圆圈)及其来自s$ _{1/2} $轨道的贡献(蓝色空心圆圈)、来自s$ _{1/2} $轨道UL-terms 的贡献(红色点圈);(b)$N\!=\!32$同中子素链及54Ca质子单粒子能级。具体细节见文献[97]。
图 8 (在线彩图)实验及协变密度泛函理论给出的(a)质子壳隙(MeV)和(b)费米面附近的质子赝自旋-轨道(PSO)劈裂
$ \Delta E_{\rm{PSO}} $ (MeV)。具体细节见正文,图取自文献[54]图 9 (在线彩图)PKA1、PKO3与DD-ME2计算得到的(a)208Pb质子赝自旋-轨道劈裂
$ \Delta $ E$ ^\pi_{PSO} $ 随赝轨道角动量$ l^\prime $ 的演化,(b)同位旋标量$ {\sigma{\rm{-S}} } $ 与$ {\omega\rm{-V} } $ 耦合以及动能项对$ \Delta $ E$ ^\pi_{\rm{PSO}} $ 的贡献。$ 1.0\kappa_\rho $ 和$ 0.0\kappa_{\rho} $ 标记着基于PKA1实验性有效拉氏量,具体细节见正文。图取自文献[54]图 10 (在线彩图)有效拉氏量PKA1、PKO3与DD-ME2中耦合强度(a)
$ g_\sigma $ 与$ g_\omega $ 、(b)$ g_\rho $ ,以及(c)$\kappa_\rho\!=\!f_\rho/g_\rho(0)$ 与$ f_\pi $ 随密度$ \rho_b $ (fm–3) 的变化。图取自文献[54]图 11 (在线彩图)超重核304120质子(a)和中子(b)单粒子能谱,采用的有效拉氏量包括RMF的PKDD与DD-ME2、RHF的PKO
$ i $ ($i\!=\!1,2,3$ )与PKA1。图取自文献[94] -
[1] OGANESSIAN Y T, UTYONKOV V K, LOBANOV Y V, et al. Phys Rev C, 2004, 69: 054607. doi: 10.1103/PhysRevC.69.054607 [2] OGANESSIAN Y T, UTYONKOV V K, LOBANOV Y V, et al. Phys Rev C, 2006, 74: 044602. doi: 10.1103/PhysRevC.74.044602 [3] OGANESSIAN Y T, ABDULLIN F S, BAILEY P D, et al. Phys Rev Lett, 2010, 104: 142502. doi: 10.1103/PhysRevLett.104.142502 [4] OGANESSIAN Y, UTYONKOV. Nucl Phys A, 2015, 944: 62. doi: 10.1016/j.nuclphysa.2015.07.003 [5] ELLISON P A, GREGORICH K E, BERRYMAN J S, et al. Phys Rev Lett, 2010, 105: 182701. doi: 10.1103/PhysRevLett.105.182701 [6] HOFMANN S, HEINZ S, MANN R, et al. Eur Phys J A, 2012, 48: 62. doi: 10.1140/epja/i2012-12062-1 [7] MENG J, TANIHHATA I, YAMAJI S. Phys Lett B, 1998, 419: 1. doi: 10.1016/s0370-2693(97)01386-5 [8] MENG J, RING P. Phys Rev Lett, 1998, 80: 460. doi: 10.1103/PhysRevLett.80.460 [9] MENG J, TOKI H, ZENG J Y, et al. Phys Rev C, 2002, 65: 041302. doi: 10.1103/PhysRevC.65.041302 [10] TANIHATA I, HAMAGAKI H, HASHIMOTO O, et al. Phys Rev Lett, 1985, 55: 2676. doi: 10.1103/PhysRevLett.55.2676 [11] WARNER R E, KELLEY J H, ZECHER P, et al. Phys Rev C, 1995, 52: R1166. doi: 10.1103/PhysRevC.52.R1166 [12] YOSHIDA A, AOI N, FUKUDA T, et al. Nucl Phys A, 1995, 588: 109c. doi: 10.1016/0375-9474(95)00108-D [13] JENSEN A, RⅡSAGER K, FEDOROV D, et al. Rev Mod Phys, 2004, 76: 215. doi: 10.1103/RevModPhys.76.215 [14] ZHUKOV M, DANILIN B, FEDOROV D, et al. Phys Rep, 1993, 231: 151. doi: 10.1016/0370-1573(93)90141-Y [15] ANNE R, ARNELL S, BIMBOT R, et al. Phys Lett B, 1990, 250: 19. doi: 10.1016/0370-2693(90)91147-4 [16] RⅡSAGER K. Rev Mod Phys, 1994, 66: 1105. doi: 10.1103/RevModPhys.66.1105 [17] ZHOU S G, MENG J, RING P. Phys Rev Lett, 2003, 91: 262501. doi: 10.1103/PhysRevLett.91.262501 [18] LI L L, MENG J, RING P, et al. Phys Rev C, 2012, 85: 024312. doi: 10.1103/PhysRevC.85.024312 [19] SUN X X, ZHAO J, ZHOU S G. Phys Lett B, 2018, 785: 530. doi: 10.1016/j.physletb.2018.08.071 [20] FRAUENDORF S, MENG J. Nucl Phys A, 1997, 617: 131. doi: 10.1016/S0375-9474(97)00004-3 [21] VAMAN C, FOSSAN D B, KOIKE T, et al. Phys Rev Lett, 2004, 92: 032501. doi: 10.1103/PhysRevLett.113.032501 [22] PETRACHE C, BAZZACCO D, LUNARDI S, et al. Nucl Phys A, 1996, 597: 106. doi: 10.1016/0375-9474(95)00416-5 [23] DIMITROV V I, FRAUENDORF S, DÖNAU F. Phys Rev Lett, 2000, 84: 5732. doi: 10.1103/PhysRevLett.84.5732 [24] STAROSTA A, KOIKE T, CHIARA C J, et al. Phys Rev Lett, 2001, 86: 971. doi: 10.1103/PhysRevLett.86.971 [25] LIU C, WANG S Y, BARK R A, et al. Phys Rev Lett, 2016, 116: 112501. doi: 10.1103/PhysRevLett.116.112501 [26] KUTI I, CHEN Q B, TIMÁR, et al. Phys Rev Lett, 2014, 113: 032501. doi: 10.1103/PhysRevLett.105.032501 [27] GRODNER E, SREBRNY J, PASTERNAK A A, et al. Phys Rev Lett, 2006, 97: 172501. doi: 10.1103/PhysRevLett.97.172501 [28] GAITANOS T, COLONNA M, TORO M D, et al. Phys Lett B, 2004, 595: 209. doi: 10.1016/j.physletb.2004.05.080 [29] TIMÁR J, VAMAN C, STAROSTA K, et al. Phys Rev C, 2006, 73: 011301. doi: 10.1103/PhysRevC.73.011301 [30] WANG S Y, QI B, LIU L, et al. Phys Lett B, 2011, 703: 40. doi: 10.1016/j.physletb.2011.07.055 [31] MENG J, PENG J, ZHANG S Q, et al. Phys Rev C, 2006, 73: 037303. doi: 10.1103/PhysRevC.73.037303 [32] YAO J M, QI B, ZHANG S Q, et al. Phys Rev C, 2009, 79: 067302. doi: 10.1103/PhysRevC.79.067302 [33] LI J, ZHANG S Q, MENG J. Phys Rev C, 2011, 83: 037301. doi: 10.1103/PhysRevC.83.037301 [34] QI B, JIA H, ZHANG N B, et al. Phys Rev C, 2013, 88: 027302. doi: 10.1103/PhysRevC.88.027302 [35] AYANGEAKAA A D, GARG U, ANTHONY M D, et al. Phys Rev Lett, 2013, 110: 172504. doi: 10.1103/PhysRevLett.110.172504 [36] OZAWA A, KOBAYASHI T, SUZUKI T, et al. Phys Rev Lett, 2000, 84: 3. doi: 10.1103/PhysRevLett.84.5493 [37] OTSUKA T, FUJIMOTO R, UTSUNO Y, et al. Phys Rev Lett, 2001, 87: 082502. doi: 10.1103/PhysRevLett.87.082502 [38] JANSSENS R, FORNAL B, MANTICA P, et al. Phys Lett B, 2002, 546: 55. doi: 10.1016/s0370-2693(02)02682-5 [39] LIDDICK S N, MANTICA P F, JANSSENS R V F, et al. Phys Rev Lett, 2004, 92: 072502. doi: 10.1103/PhysRevLett.92.072502 [40] STEPPENBECK D, TAKEUCHI S, AOI N, et al. Nature, 2013, 502: 207. doi: 10.1038/nature12522 [41] WIENHOLTZ F, BECK D, BLAUM K, et al. Nature, 2013, 498: 346. doi: 10.1016/0370-2693(95)00012-A [42] XU X, WANG M, ZHANG Y H, et al. Chin Phys C, 2015, 39: 104001. doi: 10.1088/1674-1137/39/10/104001 [43] MICHIMASA S, KOBAYASHI M, KIYOKAWA Y, et al. Phys Rev Lett, 2018, 121: 022506. doi: 10.1103/PhysRevLett.121.022506 [44] XU X, WANG M, BLAUM K, et al. Phys Rev C, 2019, 99: 064303. doi: 10.1103/PhysRevC.99.064303 [45] MAYER M G. Phys Rev, 1948, 74: 235. doi: 10.1103/PhysRev.74.235 [46] HAXEL O, JENSEN J H D, SUESS H E. Phys Rev, 1949, 75: 1766. doi: 10.1103/PhysRev.75.1766.2 [47] HAXEL O, JENSEN J H D, SUESS H E. Z. Physik, 1950, 128: 295. doi: 10.1007/BF01333077 [48] YUKAWA H. Proc Phys Math Soc Japan, 1935, 17: 48. doi: 10.1143/PTPS.1.1 [49] SHEN S H, LIANG H Z, LONG W H, et al. Prog Part Nucl Phys, 2019, 109: 103713. doi: 10.1016/j.ppnp.2019.103713 [50] VAUTHERIN D, BRINK D M. Phys Rev C, 1972, 5: 626. doi: 10.1103/PhysRevC.5.626 [51] DECHARGE J, GOGNY D. Phys Rev C, 1980, 21: 1568. doi: 10.1103/PhysRevC.21.1568 [52] WALECKA J. Ann Phys, 1974, 83: 491. doi: 10.1016/0003-4916(74)90208-5 [53] MILLER L D. Phys Rev C, 1974, 9: 537. doi: 10.1103/PhysRevC.9.537 [54] GENG J, LI J J, LONG W H, et al. Phys Rev C, 2019, 100: 051301. doi: 10.1103/PhysRevC.100.051301 [55] BOGUTA J, BODMER A R. Nucl Phys A, 1977, 292: 413. doi: 10.1016/0375-9474(77)90626-1 [56] SUGAHARA Y, TOKI H. Nucl Phys A, 1994, 579: 557. doi: 10.1016/0375-9474(94)90923-7 [57] REINHARD P G, RUFA M, MARUHN J, et al. Z Phys A - Atom Nucl, 1986, 323: 13. doi: 10.1007/BF01294551 [58] REINHARD P G. Rep Prog Phys, 1989, 52: 439. doi: 10.1088/0034-4885/52/4/002 [59] SATPATHY L, PATRA S K. Nucl Phys A, 2003, 722: C24. doi: 10.1016/S0375-9474(03)01330-7 [60] SHARMA M, NAGARAJAN M, RING P. Phys Lett B, 1993, 312: 377. doi: 10.1016/0370-2693(93)90970-S [61] LONG W H, MENG J, GIAI N V, et al. Phys Rev C, 2004, 69: 034319. doi: 10.1103/PhysRevC.69.034319 [62] ZHAO P W, LI Z P, YAO J M, et al. Phys Rev C, 2010, 82: 054319. doi: 10.1103/PhysRevC.82.054319 [63] BROCKMANN R, TOKI H. Phys Rev Lett, 1992, 68: 3408. doi: 10.1103/PhysRevLett.68.3408 [64] TYPEL S, WOLTER H H. Nucl Phys A, 1999, 656: 331. doi: 10.1016/S0375-9474(99)00310-3 [65] NIKSIC T, VRETENAR D, FINELLI P, et al. Phys Rev C, 2002, 66: 024306. doi: 10.1103/PhysRevC.98.024306 [66] LALAZISSIS G A, NIKSIC T, VRETENAR D, et al. Phys Rev C, 2005, 71: 024312. doi: 10.1103/PhysRevC.71.024312 [67] VRETENAR D, NIKSIC T, RING P. Phys Rev C, 2003, 68: 024310. doi: 10.1103/PhysRevC.68.024310 [68] SAGAWA H, YOSHIDA S, ZENG G M, et al. Phys Rev C, 2007, 76: 034327. doi: 10.1103/PhysRevC.76.034327 [69] AGRAWAL B K, SHLOMO S, KIMAU V. Phys Rev C, 2003, 68: 031304. doi: 10.1103/PhysRevC.68.031304 [70] GINOCCHIO J N. Phys Rev Lett, 1997, 78: 4. doi: 10.1103/PhysRevLett.78.436 [71] GINOCCHIO J N. Phys Rep, 2005, 414: 165. doi: 10.1016/j.physrep.2005.04.003 [72] LIANG H Z, MENG J, ZHOU S G. Phys Rep, 2015, 570: 1. doi: 10.1016/j.physrep.2014.12.005 [73] MENG J, TOKI H, ZHOU S G, et al. Prog Part Nucl Phys, 2006, 57: 470. doi: 10.1016/j.ppnp.2005.06.001 [74] NIKSIC T, VRETENAR D, RING P. Prog Part Nucl Phys, 2011, 66: 519. doi: 10.1016/j.ppnp.2011.01.055 [75] RING P. Prog Part Nucl Phys, 1996, 37: 193. doi: 10.1016/0146-6410(96)00054-3 [76] MENG J. Relativistic Density Functional for Nuclear Structure, Vol. 10[M]. New Jersey: World Scientific, 2016. [77] GENG L S, MENG J, HIROSHI T, et al. Chin Phys Lett, 2006, 23: 1139. doi: 10.1139/cjp-2016-0465 [78] SUN M D, LIU Z, HUANG T H, et al. Phys Lett B, 2017, 771: 303. doi: 10.1016/j.physletb.2017.03.074 [79] BOUYSSY A, MARCOS S, MATHIOT J F, et al. Phys Rev Lett, 1985, 55: 1731. doi: 10.1103/physrevlett.55.1731 [80] BOUYSSY A, MATHIOT J F, GIAI N V, et al. Phys Rev C, 1987, 36: 380. doi: 10.1103/PhysRevC.36.380 [81] LONG W H, GIAI N V, MENG J. Phys Lett B, 2006, 640: 150. doi: 10.1016/j.physletb.2006.07.064 [82] LONG W H, SAGAWA H, GIAI N V, et al. Phys Rev C, 2007, 76: 034314. doi: 10.1103/PhysRevC.76.034314 [83] LONG W H, SAGAWA H, MENG J, et al. Europhys Lett, 2008, 82: 12001. doi: 10.1209/0295-5075/82/12001 [84] LONG W H, RING P, GIAI N V, et al. Phys Rev C, 2010, 81: 024308. doi: 10.1103/PhysRevC.81.024308 [85] LONG W H, NAKATSUKASA T, SAGAWA H, et al. Phys Lett B, 2009, 680: 428. doi: 10.1016/j.physletb.2013.02.043 [86] WANG L J, DONG J M, LONG W H. Phys Rev C, 2013, 87: 047301. doi: 10.1103/PhysRevC.87.047301 [87] LONG W H, SAGAWA H, MENG J, et al. Phys Lett B, 2006, 639: 242. doi: 10.1016/j.physletb.2006.05.065 [88] LONG W H, RING P, MENG J, et al. Phys Rev C, 2010, 81: 031302. doi: 10.1103/PhysRevC.81.031302 [89] JIANG L J, YANG S, SUN B Y, et al. Phys Rev C, 2015, 91: 034326. doi: 10.1103/PhysRevC.91.034326 [90] LIANG H Z, GIAI N V, MENG J. Phys Rev Lett, 2008, 101: 122502. doi: 10.1103/PhysRevLett.101.122502 [91] LIANG H Z, ZHAO P W, MENG J. Phys Rev C, 2012, 85: 064302. doi: 10.1103/PhysRevC.85.064302 [92] NIU Z M, NIU Y F, LIANG H Z, et al. Phys Lett B, 2013, 723: 172. doi: 10.1016/j.physletb.2013.04.048 [93] NIU Z M, NIU Y F, LIANG H Z, et al. Phys Rev C, 2017, 95: 044301. doi: 10.1103/PhysRevC.95.044301 [94] LI J J, LONG W H, MARGUERON J, et al. Phys Lett B, 2014, 732: 169. doi: 10.1016/j.physletb.2014.03.031 [95] LI J J, MARGUERON J, LONG W H, et al. Phys Lett B, 2016, 753: 97. doi: 10.1016/j.physletb.2015.12.004 [96] LI J J, LONG W H, MARGUERON J, et al. Phys Lett B, 2019, 788: 192. doi: 10.1016/j.physletb.2018.11.034 [97] LIU J, NIU Y F, LONG W H. arXiv: 1908.08177[nucl-th](2019). [98] LI J J, LONG W H, MARGUERON J, et al. J Phys: Conf Ser, 2014, 533: 012002. doi: 10.1088/1742-6596/533/1/012002 [99] SUN B Y, LONG W H, MENG J, et al. Phys Rev C, 2008, 78: 065805. doi: 10.1103/PhysRevC.78.065805 [100] LONG W H, SUN B Y, HAGINO K, et al. Phys Rev C, 2012, 85: 025806. doi: 10.1103/PhysRevC.85.025806 [101] OTSUKA T, SUZUKI T, FUJIMOTO R, et al. Phys Rev Lett, 2005, 95: 232502. doi: 10.1103/PhysRevLett.95.232502 [102] ROCA-MAZA X, VIÑAS X, CENTELLES M, et al. Phys Rev C, 2011, 84: 054309. doi: 10.1103/PhysRevC.84.054309 [103] STEPPENBECK D, TAKEUCHI S, AOI N, et al. Phys Rev Lett, 2015, 114: 252501. doi: 10.1103/PhysRevLett.121.252501 [104] TODD-RUTEL B G, PIEKAREWICZ J, COTTLE P D. Phys Rev C, 2004, 69: 021301. doi: 10.1103/PhysRevC.69.021301 [105] OTSUKA T, GADE A, SORLIN O, et al. arXiv: 1805.06501[nucl-th](2018). [106] BURGUNDER G, SORLIN O, NOWACHI F, et al. Phys Rev Lett, 2014, 112: 042502. doi: 10.1103/PhysRevLett.112.042502 [107] LI J J, LONG W H, SONG L J, et al. Phys Rev C, 2016, 93: 054312. doi: 10.1103/PhysRevC.97.054312 [108] MUTSCHLER A, LEMASSON A, SORLIN O, et al. Nature Phys, 2017, 13: 152. doi: 10.1038/nphys3916 [109] ROSENBUSCH M, ASCHER P, ATANASOV D, et al. Phys Rev Lett, 2015, 114: 202501. doi: 10.1103/PhysRevLett.114.202501 [110] SHARMA M M, LALAZISSIS G A, RING P. Phys Lett B, 1993, 317: 9. doi: 10.1016/0370-2693(93)91561-Z [111] ZHOU S G. Proceedings of Science, 2016, 281: 373. doi: 10.22323/1.281.0373 [112] RUIZ GARCIA R F, BISSELL M L, BLAUM K, et al. Nature Phys, 2016, 12: 594. doi: 10.1038/nphys3645 [113] DUDEK J, NAZAREWICZ W, SZYMANSKI Z, et al. Phys Rev Lett, 1987, 59: 1405. doi: 10.1103/PhysRevLett.59.1405 [114] NAZAREWICZ W, TWIN P J, FALLON P, et al. Phys Rev Lett, 1990, 64: 1654. doi: 10.1103/PhysRevLett.64.1654 [115] ZENG J Y, MENG J, WU C S, et al. Phys Rev C, 1991, 44: R1745(R). doi: 10.1103/PhysRevC.44.R1745 [116] HAMAMOTO I, MOTTELSON B. Phys Lett B, 1994, 333: 294. doi: 10.1016/0370-2693(94)90144-9 [117] MENG J, SUGAWARA-TANABE K, YAMAJI S, et al. Phys Rev C, 1998, 58: R628. doi: 10.1103/physrevc.58.r628 [118] SHEN S H, LIANG H Z, ZHAO P W, et al. Phys Rev C, 2013, 88: 024311. doi: 10.1103/PhysRevC.88.024311 [119] BERGER J F, GIROD M, GOGNY D. Nucl Phys A, 1984, 428: 23. doi: 10.1016/0375-9474(84)90240-9 [120] GENG J, XIANG J, SUN B Y, et al. Phys Rev C, 2020, 101: 064302. doi: 10.1103/PhysRevC.101.064302 [121] ZHOU S G, MENG J, RING P. Phys Rev C, 2003, 68: 034323. doi: 10.1103/PhysRevC.68.034323 [122] WANG Z H, XIANG J, LONG W H, et al. J Phys G, 2015, 42: 045108. doi: 10.1088/0954-3899/42/4/045108 -





 下载:
下载:






















































































































































































































































































































































































































































































































 甘公网安备 62010202000723号
甘公网安备 62010202000723号