-
质子电荷半径的测量通常可从氢原子光谱测量实验和电子质子弹性散射实验中得到。基于一系列此类实验的平均结果，质子半径的标准值
$ r_{\rm{p}} \!=\! 0.8751(61)\,{\rm{fm}} $ 被国际数据委员会(CODATA)确定并收录[1]。2010–2013年间，瑞士保罗谢勒研究所的CREMA实验合作组通过测量$ \mu $ 氢原子光谱中的兰姆位移(2S-2P原子能级跃迁)将质子半径的测量精确度提高了一个数量级[2-3]。然而该实验结果$ r_{\rm{p}} \!=\! 0.84087(39)\,{\rm{fm}} $ 比原先CODATA标准值小$ 4\% $ ，并相差5.6个标准差($ 5.6\sigma $ )。这个发现引起了理论和实验物理学家的广泛关注。$ \mu $ 氢原子实验与传统实验结果间的惊人差异可能源于实验中被忽略的系统误差，或是来自原子光谱理论中未考虑到的量子电动力学(QED)高阶修正，甚至可能由超出标准模型的轻子普适性破缺所导致。为了破解质子半径之谜的难题，理论和实验物理学家已做出了多种尝试。其中一个研究方向是重新检验氢原子光谱实验测得质子半径的系统误差。最近，测量氢原子
$ 2S $ -$ 2P $ ，$ 2S $ -$ 4P $ 和$ 1S $ -$ 3S $ 能级跃迁的三个新实验中[4-6]获得的质子半径结果相互矛盾。前两者与$ \mu $ 氢原子实验符合，后者与CODATA推荐值一致。另一方面，最新的电子-质子散射实验中得到比CODATA值小$ 5\% $ 的质子半径，与$ \mu $ 氢原子实验结果一致[7]。此外，CREMA合作组将$ \mu $ 氢原子实验扩展到其他$ \mu $ 原子中[8]。在$ \mu $ 氘原子($ \mu^2 {\rm{H}} $ )和$ \mu $ 氦离子($ \mu^{3,4} {\rm{He}}^+ $ )中进行的一系列兰姆位移测量旨在获得相应轻核的电荷半径。通过比较$ \mu $ 原子实验中得到的核半径与普通原子光谱、电子-核散射实验之间的差异，并追踪此差距随原子核中质子数与中子数的变化，我们可以了解质子半径之谜中存在的规律，并发现破解迷题的重要线索。在原子光谱实验中，对兰姆位移的测量已可达到相当高的精度。但要从原子能谱数据中提取出核半径的大小仍然依赖于理论的输入。因此对兰姆位移的理论计算也需要达到很高的准确度。这些理论输入量包括QED与核结构效应对原子能谱的修正。由于
$ \mu $ 子比电子重200倍，$ \mu $ 子在轻子-核系统中绕核运动的平均距离比电子短约200倍。因此，核结构修正对$ \mu $ 原子能谱的贡献要远大于它对普通原子的贡献[9]。在$ \mu $ 原子中，兰姆位移$ \delta_{\rm{LS}} $ 与核电荷半径$ r_{\rm{E}} $ 之间的关系可表示为$$ \delta_{\rm{LS}} = \delta_{\rm{QED}} + {\cal{A}}_{\rm{OPE}}\, r^2_{\rm{E}} + \delta_{\rm{TPE}}, $$ (1) 第一项
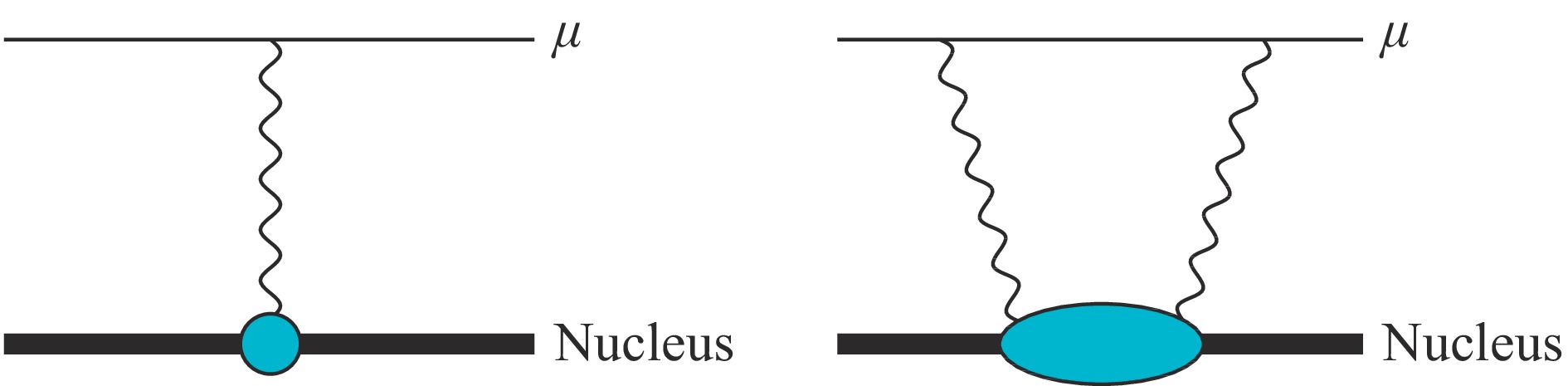
$ \delta_{\rm{QED}} $ 是QED的贡献值，后两项均来自核结构修正。在图1中，核结构修正对应于由$ \mu $ 子与原子核之间的单光子交换(one-photon exchange, 简称OPE)和双光子交换(two-photon exchange，简称TPE)对$ \mu $ 原子能谱的影响。单光子交换项正比于核半径的平方$ r^2_{\rm{E}} $ 。系数$ {\cal{A}}_{\rm{OPE}} $ 约等于$ m_{r}^3(Z\alpha)^4/12 $ ，其中$ m_r $ 为$ \mu $ 子-原子核质心系约化质量，$ Z $ 为核内质子数，$ \alpha $ 为精细结构常数。$ {\cal{A}}_{\rm{OPE}} $ 的精确值可由QED理论计算得到。双光子交换项$ \delta_{\rm{TPE}} $ 的数量级为$ (Z\alpha)^5 $ ，对它的估值依赖于核结构理论与光核反应的计算。
图 1 (在线彩图)
$ \mu$ 子与原子核间的单/双光子交换过程式(1)将兰姆位移
$ \delta_{\rm{LS}} $ 的测量数据与理论计算连接，从而提取出核半径$ r_{\rm{E}} $ 。为了能够在精度上区分普通原子光谱与$ \mu $ 原子光谱测量中$ r_{\rm{E}} $ 的结果，我们对$ \delta_{\rm{LS}} $ 的理论计算也需要非常准确。当前的研究瓶颈主要取决于双光子交换项$ \delta_{\rm{TPE}} $ 的理论预测精度。本文将介绍我们最近在一系列$ \mu $ 原子中计算$ \delta_{\rm{TPE}} $ 的最新进展[10-15]。该理论工作运用了原子核多体理论中的从头算计算方法。该方法在过去几十年中得到了长足的发展。 -
双光子交换对
$ \mu $ 原子能级的修正($ \delta_{\rm{TPE}} $ )可通过色散关系与光核反应截面以及虚光子的康普顿散射振幅建立关联[16-19]。$ \delta_{\rm{TPE}} $ 可进一步分解为弹性与非弹性部分，被分别称为Zemach项和核极化项，$ \delta_{\rm{TPE}} \!=\! \delta_{\rm{Zem}} + \delta_{\rm{pol}} $ 。Zemach项$ \delta_{\rm{Zem}} $ 对应于双光子交换中核或核子本身始终处于基态的贡献部分，它与原子核电荷密度的卷积相关联[20-21]，$$ \delta_{\rm{Zem}} = - \frac{m_r^4(Z\alpha)^5 }{24} \int {\rm{d}}^3 r \int {\rm{d}}^3 r'\, r^3 \rho_{\rm E}({{r}}-{{r}}')\rho_{\rm E}({{r}}')\text{。} $$ (2) 核极化项
$ \delta_{\rm{pol}} $ 反映了在双光子交换中核或核子被激发再退激发时对$ \mu $ 原子能级的影响。轻核与核子的激发能分别约为30和300 MeV，两者相差一个数量级。根据有效场论中的尺度分离原理，我们可以用不同自由度下的有效理论分别描述$ \delta_{\rm{pol}} $ 中核与核子的极化贡献。因此，$ \delta_{\rm{pol}} $ 可拆分为$ \delta_{\rm{pol} } \!=\! \delta_{\rm{pol}}^A + \delta_{\rm{pol}}^N $ 。上标$ A $ 和$ N $ 分别代表核与核子的贡献。同理，$ \delta_{\rm{Zem}} \!=\! \delta_{\rm{Zem}}^A + \delta_{\rm{Zem}}^N $ ，$ \delta_{\rm{TPE}} \!=\! \delta_{\rm{TPE}}^A + \delta_{\rm{TPE}}^N $ 。从头算理论的运用是为了计算双光子交换中核的部分($ \delta_{\rm{TPE}}^A \!=\! \delta_{\rm{Zem}}^A+\delta_{\rm{pol}}^A $ )。该理论将原子核描述为多个核子间相互作用的多体系统，并运用量子多体计算方法来描述核的结构特征与反应机制。计算
$ \delta_{\rm{TPE}}^A $ 的关键要素是一系列包含不同能量加权函数$ g(\omega) $ 与核响应函数$ S_{\hat O}(\omega) $ 的广义求和规则(Generalized Sum Rule，简称GSR)$$ \Sigma_{\rm{GSR}} = \int_{\omega_{\rm{th}}}^{\infty} {{{\rm{d}}}} \omega \, g(\omega) S_{\hat O}(\omega)\text{。} $$ (3) 在这些求和规则中，最主要的贡献来自电偶极核响应函数，其能量权重与
$ \sqrt {m_r / \omega} $ 成比例。$ \omega $ 对应核的激发能。使用Lanczos算法(Lanczos Algorithm)，我们可以快速有效地计算GSR[22]。Lanczos算法将GSR在一组离散的束缚态完备基矢下展开，并对多核子系统的哈密顿量进行快速的数值对角化。在双核子系统中，我们通常使用球谐振子基矢展开哈密顿量。在三核子和四核子系统中，我们运用超球简谐完备基展开GSR。通过相似性重整变换，我们运用有效相互作用下的超球简谐基(Effective Interaction Hyperspherical Harmonics，EIHH)[23-24]，得到数值计算上更高效率的收敛结果。双光子交换中核子的部分
$ \delta_{\rm{TPE}}^N $ 超出了从头算理论预测的适用范围。因为该理论中没有包含核子内部结构的自由度。$ \mu {\rm{H}} $ 中$ \delta_{\rm{TPE}}^N $ 的值可通过色散关系对电子-质子散射实验数据进行分析而得到[16-17]。$ \delta_{\rm{TPE}}^N $ 在其他$ \mu $ 原子中的大小与它在$ \mu {\rm{H}} $ 中的值成正比。其中Zemach项$ \delta_{\rm{Zem}}^N $ 的比例与式 (2)的系数以及原子核的质子数$ Z $ 直接相关(中子Zemach项可忽略不计)，而极化项$ \delta_{\rm{pol}}^N $ 的比例关系与原子波函数的归一化因子以及原子核的核子数$ A $ 直接相关(质子与中子均可极化)。因此可直接利用它们之间的比例关系得到其他$ \mu $ 原子中的$ \delta_{\rm{TPE}}^N $ 。$$ \delta_{\rm{Zem}}^N (\mu {\rm{X}}) = \left[\frac{Z m_r(\mu{}{\rm{X}})}{m_r(\mu {\rm{H}})}\right]^4 \delta_{\rm{Zem}}^{N} (\mu {\rm{H}})\text{。} $$ (4) $$ \delta_{\rm{pol}}^N (\mu{}{\rm{X}}) = A \left[\frac{Z m_r(\mu{}{\rm{X}})}{m_r(\mu {\rm{H}})}\right]^3 \delta_{\rm{pol}}^N (\mu {\rm{H}})\text{。} $$ (5) 这一结果与直接通过色散关系分析电子-轻核散射数据获得的结果一致[18-19]。
$ \delta_{\rm{TPE}} $ 在不同$ \mu $ 原子中贡献的详细计算可在我们最近的综述文献[14]中找到。 -
我们使用了一系列不同参数化的手征有效场(
$ \chi $ EFT)核力来计算$ \mu^2 {\rm{H}} $ 中的$ \delta_{\rm{TPE}} $ [10-11]。在$ \chi $ EFT各参数化计算下的平均值与唯象势能模型[25-26](Argonne V18，AV18)和零力程核力模型[15,27](Zero-Range Interaction)下的计算结果高度一致，并且也符合色散关系分析下的结果[18]。基于有效场下的幂数展开原理，核力在低能附近的逐阶展开可用于分析手征核力的理论精度。在$ \mu^2 {\rm{H}} $ 中，$ \delta_{\rm{TPE}} $ 中由核力模型的不确定度产生的理论误差为$ 0.6\% $ 。作为对比，由于在低动量和小散射角范围内缺乏高精度的电子-氘核准弹性散射数据，色散关系分析下的结果的不确定性为$ 20\% $ ，远大于$ \chi $ EFT计算的不确定度。CREMA合作组在2016年发表了
$ \mu^2 {\rm{H}} $ 兰姆位移的测量结果，并从中提取出氘核的电荷半径$ r_{\rm{d}} \!=\! 2.12562(78) $ fm[28]。它的系统误差主要来源于$ \delta_{\rm{TPE}} $ 理论预测的不确定性。这一新的氘核半径结果比CODATA标准值[1]小$ 6.0 \sigma $ 。它与$ e^2 {\rm{H}} $ 原子光谱测量中的结果[29]也相差$ 3.5 \sigma $ 。同时，$ \mu {\rm{H}} - \mu^2 {\rm{H}} $ 的核半径同位素位移$ r_{\rm{d}}^2-r_{\rm{p}}^2 $ 的测量值$ e {\rm{H}} - e^2 {\rm{H}} $ 的结果相差$ 2.6\sigma $ [30]。最近，我们重新研究了
$ \mu^2 {\rm{H}} $ 能谱中双光子交换的贡献部分，分析了源自$ \chi $ EFT理论的不确定度[11]。多参数协同拟合优化的方法[31]，我们发现$ \chi $ EFT中参数拟合的统计误差相比于$ \chi $ EFT本身的系统误差可忽略不计。系统误差可由$ \chi $ EFT中的核力在幂数展开下逐阶收敛性(从领头阶到第4次领头阶)来估算。我们发现$ \delta_{\rm{TPE}} $ 的系统误差在运用参数协同优化的手征核力下的结果与未做统计优化的手征核力下的计算近乎一致，两者均偏离从$ \mu^2 {\rm{H}} $ 实验中直接提取出的$ \delta_{\rm{TPE}} $ 数值。在过去的六年中，我们运用从头算理论预测了
$ \mu^3 $ H，$ \mu^{3,4} $ He$ ^{+} $ 中的$ \delta_{\rm{TPE}} $ [12-13]。我们可以完整分析这些$ \mu $ 原子中由于核结构理论的不确定性对$ \delta_{\rm{TPE}} $ 产生的系统误差。在这些计算中，我们采用了两种核力模型。一种是唯象两体/三体核力AV18+UIX[32-33]；另一种是具有某一特定参数化的两体/三体手征核力$ \chi $ EFT[34-35]。运用多体计算，我们可以研究三核子和四核子系统在不同核力下的动力学性质，及与$ \mu $ 子间的双光子交换过程。综合大量彼此独立的理论工作，CREMA合作组总结了QED和核结构效应对
$ \mu^{3,4} {\rm{He}}^+ $ 中兰姆位移的贡献[36-37]。这为未来分析实验数据并确定$ {}^{3,4} {\rm{He}} $ 的核半径提供了准备。这些实验还可用于准确获得氦核半径的同位素位移，因而引起了原子物理学家们极大的兴趣与关注[38]。我们在表1中列出了不同
$ \mu $ 原子中$ \delta_{\rm{TPE}} $ 在从头算理论下的预测结果和理论误差[14]，并分解为弹性部分和非弹性部分，以及原子核部分和核子部分。从表中可见，$ \delta_{\rm{TPE}} $ 中核子部分的贡献通常小于相应的原子核的贡献。因此，计算原子核的双光子交换贡献并分析其理论误差具有重要价值。我们发现从$ \mu^2 {\rm{H}} $ 到$ \mu^{3,4} {\rm{He}}^+ $ ，核结构模型产生的理论误差随着核的增大而逐渐增加。然而原子物理的理论误差在每个$ \mu $ 原子中差别较小。表 1 不同
$\mu$ 原子中$\delta_{\rm{TPE}}$ 的计算结果和理论误差(单位：meV)$\delta^{N}_{\rm{Zem}}$ $\delta^{N}_{\rm{pol}}$ $\delta^{A}_{\rm{Zem}}$ $\delta^{A}_{\rm{pol}}$ $\delta_{\rm{TPE}}$ $\mu^2{\rm{H}}$ –0.030(02) –0.020(10) –0.423(04) –1.245(13) –1.718(17) $\mu^3{\rm{H}}$ –0.033(02) –0.031(17) –0.227(06) –0.480(11) –0.771(22) $\mu^3{\rm{He}}^{+}$ –0.52(03) –0.25(13) $-$10.49(23) –4.23(18) –15.49(33) $\mu^4{\rm{He}}^{+}$ –0.54(03) –0.34(20) –6.14(31) –2.35(13) –9.37(44) 结果被分解为弹性部分和非弹性部分，以及原子核部分和核子部分。表来源于文献[14]。 计算
$ \delta_{\rm{TPE}} $ 并严格量化其理论误差对准确从$ \mu $ 原子实验数据中提取核半径至关重要。因此，我们研究了其理论误差的所有可能来源。对于原子核部分$ \delta_{\rm{TPE}}^A $ ，误差来自数值精度(NA)，核模型依赖性(NM)，同位旋对称性破缺(ISB)，核子结构修正(NS)，相对论修正(R)，库仑修正(C)，以及多极矩展开($ \eta $ E)和$ {Z \alpha} $ 展开的高阶修正。文献[14]对不同$ \mu $ 原子中理论误差来源做出了详细评估。表2总结了$ \delta_{\rm{TPE}}^A $ 的各项误差来源。对于核子部分$ \delta_{\rm{TPE}}^N $ ，不同$ \mu $ 原子的理论误差可通过它们与$ \mu $ H间的线性关系来估算其误差在不同$ \mu $ 原子中的改变。$ \delta_{\rm{TPE}} $ 的总误差是$ \delta^{A}_{\rm{TPE}} $ 和$ \delta^{N}_{\rm{TPE}} $ 误差的平方求和。表 2
$\delta^A_{\rm{Zem}}$ ，$\delta^A_{\rm{pol}}$ 和$\delta^A_{\rm{TPE}}$ 理论相对误差($\%$ )的各项来源$\mu^2{\rm{H}}$ $\mu^3{\rm{H}}$ $\mu^3{\rm{He}}^+$ $\mu^4{\rm{He}}^+$ $\delta_{\rm{Zem}}^A$ $\delta_{\rm{pol}}^A$ $\delta_{\rm{TPE}}^A$ $\delta_{\rm{Zem}}^A$ $\delta_{\rm{pol}}^A$ $\delta_{\rm{TPE}}^A$ $\delta_{\rm{Zem}}^A$ $\delta_{\rm{pol}}^A$ $\delta_{\rm{TPE}}^A$ $\delta_{\rm{Zem}}^A$ $\delta_{\rm{pol}}^A$ $\delta_{\rm{TPE}}^A$ NA 0.0 0.0 0.0 0.0 0.1 0.1 0.1 0.4 0.1 0.3 0.4 0.4 NM 0.5 0.3 0.4 2.4 1.3 1.7 1.8 0.7 1.5 4.6 3.9 4.4 ISB 0.2 0.2 0.2 0.2 0.7 0.5 0.2 1.8 0.5 0.5 2.2 0.5 NS 0.8 0.3 0.0 0.9 0.6 0.2 1.3 1.2 0.9 2.0 2.7 1.2 R – 0.0 0.0 – 0.1 0.1 – 0.4 0.1 – 0.1 0.0 C – 0.4 0.3 – 0.5 0.3 – 3.0 0.9 – 0.4 0.1 $\eta$E – 0.4 0.3 – 1.3 0.9 – 1.1 0.3 – 0.8 0.2 $(Z\alpha)^6$ – 0.7 0.5 – 0.7 0.5 – 1.5 0.4 – 1.5 0.4 Total 0.9 1.0 0.8 2.7 2.3 2.0 2.2 4.2 2.1 5.1 5.5 4.6 总的理论误差通过平方求和各项误差获得。表来源于文献[14]。 -
在文献[10-14]中，核极化效应的计算基于电磁多极展开，其展开因子
$ \eta $ 与核激发能以及质子在吸收与释放光子间移动的距离相关$ \eta \!=\! \sqrt{2 m_r \omega}|{{R}}-{{R}}'| $ (称之为$ \eta $ 展开)。利用测不准原理中质子移动距离与激发能的关系可估算出$ \eta\sim \sqrt{m_\mu/m_N}\approx 0.3 $ ，因此该展开具备收敛性。然而在实际计算中我们发现，$ \eta $ 展开在不同$ \mu $ 原子中的收敛速率存在差异，这与各原子核各异的激发态结构直接相关。从式 (3)可见，核极化效应的求和规则包含若干电磁多极跃迁响应函数，后者在各原子核中以及各多极跃迁中共振的位置和结构不尽相同，从而导致各$ \mu $ 原子中$ \eta $ 多极展开效率的差异性。从表1中的$ \eta{\rm{E}} $ 项可以看出，$ \eta $ 展开在次次领头阶截断的系统误差在$ \mu ^2{\rm{H}} $ 中最小(0.4%)，而在$ \mu ^3{\rm{He}} $ 中最大(1.3%)。利用核电荷、电流密度算符在低动量下的展开，可避开
$ \eta $ 展开，是计算双光子交换的另一种途径[39-40]。结合Lanczos迭代算法，我们可将这一方法(称之为$ \eta $ -less展开)用于计算核极化效应。$ \eta $ -less展开下的求和规则是动量与能量的双重积分，其中纵向极化的贡献可表示为$$ \delta_{{\rm{pol}},L} = -m_r^3 (Z\alpha)^5 \int\nolimits_0^\infty {{{\rm{d}}}}q \int\nolimits_{\omega_{\rm{th}}}^{\infty} {{{\rm{d}}}}\omega \ K_{L}(q,\omega)S_{L}(q,\omega), $$ (6) 其中
$ S_L $ 是广义纵向极化响应函数，$ K_L $ 是积分权重函数。前者在$ \eta $ -less展开下是电磁多极响应函数之和：$$ S_L(q,\omega) = \sum\limits_J^{J_{\rm{max}}} S_{L,J}(q,\omega)\text{。} $$ (7) 其中
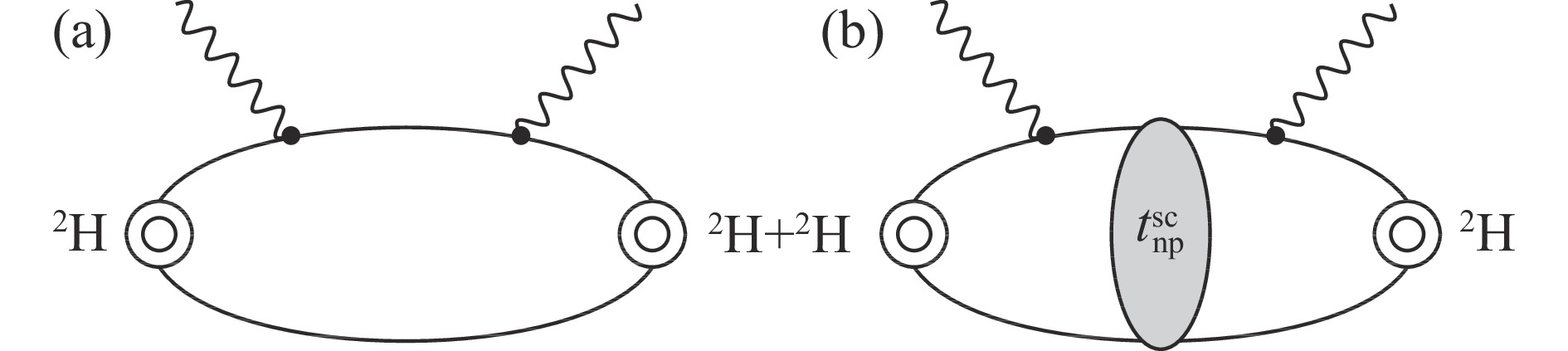
$ EJ $ 对应电多极跃迁类型(E1为电偶极跃迁)。结合式 (6)和 (7)可知，$ \eta $ -less展开需要计算众多电磁多极响应函数，因而需要较大的数值计算量。结合Lanczos迭代方法，可以直接计算求和规则，从而避开对响应函数在各动量和能量的单独求解，极大地提升了计算的效率[22]。$ \eta $ -less展开的收敛性在$ \mu^2{\rm{H}} $ 中有很好的展现[15]。利用光学原理，我们进一步证实纵向极化响应函数
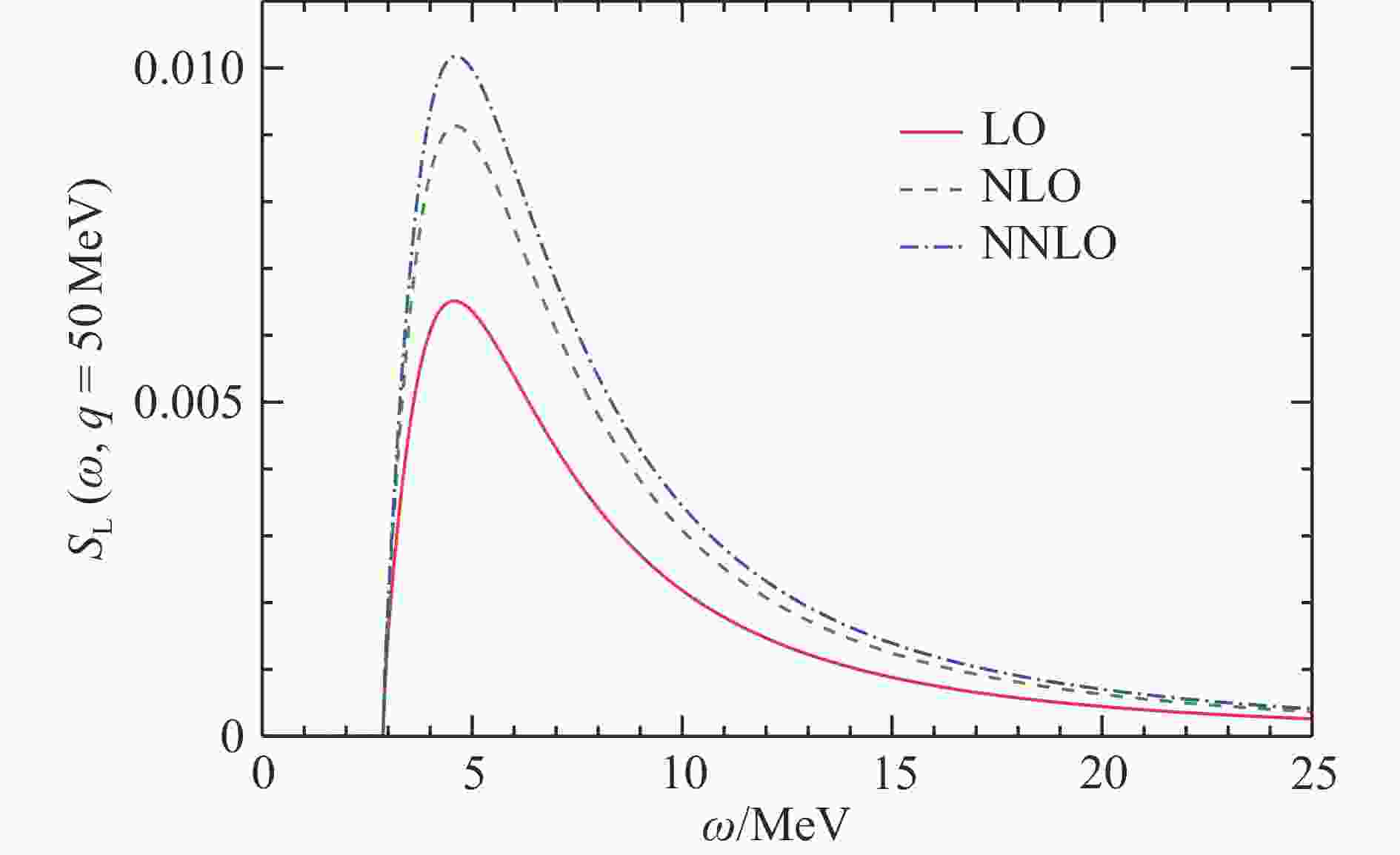
$ S_L $ 与双虚光子康普顿散射振幅的虚部直接相关。后者在2H中的振幅$ {\cal{T}}_{\mu \nu} $ 可由图2表示。我们利用无$ \pi $ 介子有效场理论($ {\not \pi } {\rm{{EFT}}} $ )分别在领头阶(LO)、次领头阶(NLO)和次次领头阶(NNLO)下求得$ ^2 $ H的纵向极化响应函数$ S_{L}(\omega,q) $ 。当固定$ q $ 后，$ S_{L} $ 随$ \omega $ 变化的函数可见图3。从图中可见，该计算在有效场理论的各阶展开下具有一致的连续收敛性。
图 2 2H双虚光子康普顿散射振幅
${\cal{T}}_{\mu \nu}$ 
图 3 (在线彩图)2H纵向极化响应函数
$S(\omega,q)$ 当$q = 50$ MeV时随$\omega$ 的变化关系为对比不同算法的结果，我们在
$ \eta $ 展开和$ \eta $ -less展开中选取零力程核子－核子相互作用模型，分别在非相对论(NR)和相对论极限下(R)下计算$ \mu^2 $ H在点状核近似下的核纵向极化效应$ \delta_{{\rm{pol}},L} $ ，并与$ {\not \pi} {\rm{EFT}} $ 下的计算结果相比较(见表3)。在$ \eta $ -less展开中，当$ J_{\rm{max}} \!=\! 12 $ 时，$ \delta_{{\rm{pol}},L} $ 收敛至与$ \eta $ 展开十分相近的结果。$ {\not \pi} {\rm{EFT}} $ 的计算结果比前两种在非相对论极限下大0.9%，在相对论极限下大0.7%。这一差别由$ {\not \pi} {\rm{EFT}} $ 中引入的高阶核反冲效应修正所导致。通过比较三种计算方法，我们验证了多极展开在计算$ \mu^2 $ H核极化效应中的收敛性与高精度。表 3 运用
$\eta$ 展开、$\eta$ -less展开和${\not \pi} {\rm{EFT}} $ 计算$\mu^2$ H核极化效应在纵向极化部分的贡献分别在非相对论(NR)和相对论极限下(R)下的结果(单位：meV)$\delta_{{\rm{pol}},L}$ $\eta$展开 $\eta$-less展开 ${\not \pi} {\rm{EFT}} $ NR –1.590 –1.590 –1.605 R –1.561 –1.562 –1.574 -
包括核极化效应在内的双光子交换是
$ \mu $ 原子实验中关键的理论输入，它决定了从$ \mu $ 原子兰姆位移测量中提取核电荷半径的精度。从头算理论对轻质量$ \mu $ 原子中的$ \delta_{\rm{TPE}} $ 贡献项做出了可靠的预测，并有效降低了理论误差。$ \mu^{2,3} {\rm{H}} $ 和$ \mu^{3,4} $ $ {\rm{He}}^+ $ 的双光子交换的理论预测已达到百分比量级的精度。高精度的理论预测将协助CREMA合作组实现对核半径和同位素位移的准确测量。这些实验将有助于揭开质子半径之谜。
Application of Photonuclear Reaction to Evaluating Nuclear Polarizability in Muonic Atoms
-
摘要: 近年来，瑞士保罗谢勒研究所的CREMA合作组通过测量
$\mu$ 氢原子兰姆位移显著提升了质子半径的测量精确度。然而这一新实验结果与已知质子半径标准值(CODATA)相差5.6个标准差，被称为质子半径之谜，受到众多物理学家的关注。受此启发，CREMA合作组在不同的$\mu$ 原子中展开了一系列兰姆位移光谱的测量实验。他们计划从这些$\mu$ 原子的测量中得到轻核(包括$^{2,3}{\rm{H}}$ ,$^{3,4}{\rm{He}}$ )的电荷半径。除了对光谱测量精度的要求外，轻核半径的实验精度当前仍被一项理论输入量限制：核极化效应对$\mu$ 原子光谱的修正。核极化效应体现了$\mu$ 子与原子核进行双光子交换中对核的虚激发，进而对$\mu$ 原子能谱产生高阶修正。因此，这一效应与光核反应以及康普顿散射直接相关。核极化效应对兰姆位移的修正可通过计算光核吸收截面以及虚光子康普顿振幅的求和规则而得到。本工作运用第一性原理的核结构计算方法，研究了$\mu$ 原子中的核极化效应。通过结合现代核力模型与超球简谐基展开多体方法，计算了一系列与核极化相关的光核反应及康普顿散射求和规则。这一理论研究为从$\mu$ 原子光谱测量中对核半径的精确提取提供了关键性的理论输入。Abstract: Recent measurements by CREMA Collaboration in Paul Scherrer Institute (Switzerland) determined the proton radius in Lamb shift spectroscopy of muonic hydrogen with a significantly improved precision. However, they discovered that this determination differs from the well-accepted CODATA value by 5.6 standard deviation. This discovery is named the “proton radius puzzle”, and attracted interests of many physicists. Inspired by this work, the CREMA Collaboration extended their experiments in muonic hydrogen to a series of light muonic atoms/ions, including$\mu^{2,3}$ H and$\mu^{3,4}$ He$^+$ . They planned to extract the radii of light nuclei (i.e., 2,3H,3,4He) from Lamb shift measurements in muonic atoms. Besides the spectroscopy precision, the accuracy of nuclear radii is limited by one theoretical input, i.e., nuclear polarizability. Nuclear polarizability originates from virtual excitation of the nucleus during the two-photon exchange process. This effect can make higher-order corrections to the muonic atom spectrum. Polarizability is strongly connected with the photonuclear reaction and the virtual Compton scattering. Therefore, its correction to the Lamb shift can be obtained by evaluating the sum rules of photoabsorption cross sections and forward virtual Compton amplitudes. Using ab initio methods, we calculated the nuclear polarizability effects in muonic atoms. By utilizing modern nuclear force models and the hyperspherical harmonic many-body approaches, we calculated a series of photonuclear sum rules, which are correlated with the nuclear polarizability. This theoretical work provides key input to the high-precision determination of nuclear radii in muonic atom spectroscopy. -
图 2 2H双虚光子康普顿散射振幅
${\cal{T}}_{\mu \nu}$ (a)与(b)分别对应双光子过程的平面波部分和末态作用部分。波浪线与实线分别代表光子与核子，双线圆圈代表2H束缚态T矩阵，$t^{\rm{sc}}_{\rm{np}}$为$np$散射态T矩阵。
图 3 (在线彩图)2H纵向极化响应函数
$S(\omega,q)$ 当$q = 50$ MeV时随$\omega$ 的变化关系实线(红色)、虚线(绿色)和点虚线(蓝色)分别对应${\not \pi} {\rm{{EFT}}} $在LO、NLO和NNLO下的结果。
表 1 不同
$\mu$ 原子中$\delta_{\rm{TPE}}$ 的计算结果和理论误差(单位：meV)$\delta^{N}_{\rm{Zem}}$ $\delta^{N}_{\rm{pol}}$ $\delta^{A}_{\rm{Zem}}$ $\delta^{A}_{\rm{pol}}$ $\delta_{\rm{TPE}}$ $\mu^2{\rm{H}}$ –0.030(02) –0.020(10) –0.423(04) –1.245(13) –1.718(17) $\mu^3{\rm{H}}$ –0.033(02) –0.031(17) –0.227(06) –0.480(11) –0.771(22) $\mu^3{\rm{He}}^{+}$ –0.52(03) –0.25(13) $-$ 10.49(23)–4.23(18) –15.49(33) $\mu^4{\rm{He}}^{+}$ –0.54(03) –0.34(20) –6.14(31) –2.35(13) –9.37(44) 结果被分解为弹性部分和非弹性部分，以及原子核部分和核子部分。表来源于文献[14]。 
下载: 导出CSV
表 2
$\delta^A_{\rm{Zem}}$ ，$\delta^A_{\rm{pol}}$ 和$\delta^A_{\rm{TPE}}$ 理论相对误差($\%$ )的各项来源$\mu^2{\rm{H}}$ $\mu^3{\rm{H}}$ $\mu^3{\rm{He}}^+$ $\mu^4{\rm{He}}^+$ $\delta_{\rm{Zem}}^A$ $\delta_{\rm{pol}}^A$ $\delta_{\rm{TPE}}^A$ $\delta_{\rm{Zem}}^A$ $\delta_{\rm{pol}}^A$ $\delta_{\rm{TPE}}^A$ $\delta_{\rm{Zem}}^A$ $\delta_{\rm{pol}}^A$ $\delta_{\rm{TPE}}^A$ $\delta_{\rm{Zem}}^A$ $\delta_{\rm{pol}}^A$ $\delta_{\rm{TPE}}^A$ NA 0.0 0.0 0.0 0.0 0.1 0.1 0.1 0.4 0.1 0.3 0.4 0.4 NM 0.5 0.3 0.4 2.4 1.3 1.7 1.8 0.7 1.5 4.6 3.9 4.4 ISB 0.2 0.2 0.2 0.2 0.7 0.5 0.2 1.8 0.5 0.5 2.2 0.5 NS 0.8 0.3 0.0 0.9 0.6 0.2 1.3 1.2 0.9 2.0 2.7 1.2 R – 0.0 0.0 – 0.1 0.1 – 0.4 0.1 – 0.1 0.0 C – 0.4 0.3 – 0.5 0.3 – 3.0 0.9 – 0.4 0.1 $\eta$ E– 0.4 0.3 – 1.3 0.9 – 1.1 0.3 – 0.8 0.2 $(Z\alpha)^6$ – 0.7 0.5 – 0.7 0.5 – 1.5 0.4 – 1.5 0.4 Total 0.9 1.0 0.8 2.7 2.3 2.0 2.2 4.2 2.1 5.1 5.5 4.6 总的理论误差通过平方求和各项误差获得。表来源于文献[14]。
下载: 导出CSV
表 3 运用
$\eta$ 展开、$\eta$ -less展开和${\not \pi} {\rm{EFT}} $ 计算$\mu^2$ H核极化效应在纵向极化部分的贡献分别在非相对论(NR)和相对论极限下(R)下的结果(单位：meV)$\delta_{{\rm{pol}},L}$ $\eta$ 展开$\eta$ -less展开${\not \pi} {\rm{EFT}} $ NR –1.590 –1.590 –1.605 R –1.561 –1.562 –1.574
下载: 导出CSV
-
[1] MOHR P J, NEWELL D B, TAYLOR B N. Rev Mod Phys, 2016, 88: 035009. doi: 10.1103/RevModPhys.88.035009 [2] POHL R, ANTOGNINI A, NEZ F, et al. Nature, 2010, 466: 213. doi: 10.1038/nature09250 [3] ANTOGNINI A, NEZ F, SCHUHMANN K, et al. Science, 2013, 339: 417. doi: 10.1126/science.1230016 [4] BEZGINOV N, VALDEZ T, HORBATSCH M, et al. Science, 2019, 365: 1007. doi: 10.1126/science.aau7807 [5] BEYER A, MAISENBACHER L, MATVEEV A, et al. Science, 2017, 358: 79. doi: 10.1126/science.aah6677 [6] FLEURBAEY H, GALTIER S, THOMAS S, et al. Phys Rev Lett, 2018, 120: 183001. doi: 10.1103/PhysRevLett.120.183001 [7] XIONG W, GASPARIAN A, GAO H, et al. Nature, 2019, 575: 147. doi: 10.1038/s41586-019-1721-2 [8] ANTOGNINI A, BIRABEN F, CARDOSO J M R, et al. Can J Phys, 2011, 89: 47. doi: 10.1139/P10-113 [9] BORIE E. Ann Phys, 2012, 327: 733. doi: 10.1016/j.aop.2011.11.017 [10] HERNANDEZ J O, JI C, BACCA S, et al. Phys Lett B, 2014, 736: 344. doi: 10.1016/j.physletb.2014.07.039 [11] HERNANDEZ O, EKSTRÖM A, NEVO D N, et al. Phys Lett B, 2018, 778: 377. doi: 10.1016/j.physletb.2018.01.043 [12] NEVO D N, JI C, BACCA S, et al. Phys Lett B, 2016, 755: 380. doi: 10.1016/j.physletb.2016.02.023 [13] JI C, NEVO D N, BACCA S, et al. Phys Rev Lett, 2013, 111: 143402. doi: 10.1103/PhysRevLett.111.143402 [14] JI C, BACCA S, BARNEA N, et al. J Phys G, 2018, 45: 093002. doi: 10.1088/1361-6471/aad3eb [15] HERNANDEZ O J, JI C, BACCA S, et al. Phys Rev C, 2019, 100: 064315. doi: 10.1103/PhysRevC.100.064315 [16] CARLSON C E, VANDERHAEGHEN M. Phys Rev A, 2011, 84: 020102. doi: 10.1103/PhysRevA.84.020102 [17] BIRSE M, MCGOVERN J. Eur Phys J A, 2012, 48: 120. doi: 10.1140/epja/i2012-12120-8 [18] CARLSON C E, GORCHTEIN M, VANDERHAEGHEN M. Phys Rev A, 2014, 89: 022504. doi: 10.1103/PhysRevA.89.022504 [19] CARLSON C E, GORCHTEIN M, VANDERHAEGHEN M. Phys. Rev. A, 2017, 95: 012506. doi: 10.1103/PhysRevA.95.012506 [20] FRIAR J. Ann Phys, 1979, 122: 151. doi: 10.1016/0003-4916(79)90300-2 [21] ZEMACH A C. Phys Rev, 1956, 104: 1771. doi: 10.1103/PhysRev.104.1771 [22] NEVO D N, BARNEA N, JI C, et al. Phys Rev C, 2014, 89: 064317. doi: 10.1103/PhysRevC.89.064317 [23] BARNEA N, LEIDEMANN W, ORLANDINI G. Phys Rev C, 2000, 61: 054001. doi: 10.1103/PhysRevC.61.054001 [24] BARNEA N, LEIDEMANN W, ORLANDINI G. Nucl Phys A, 2001, 693: 565. doi: 10.1016/S0375-9474(01)00794-1 [25] PACHUCKI K. Phys Rev Lett, 2011, 106: 193007. doi: 10.1103/PhysRevLett.106.193007 [26] PACHUCKI K, WIENCZEK A. Phys Rev A, 2015, 91: 040503. doi: 10.1103/PhysRevA.91.040503 [27] FRIAR J L. Phys Rev C, 2013, 88: 034003. doi: 10.1103/PhysRevC.88.034003 [28] POHL R, NEZ F, FERNANDES L M P, et al. Science, 2016, 353: 669. doi: 10.1126/science.aaf2468 [29] POHL R, NEZ F, UDEM T, et al. Metrologia, 2017, 54: L1. doi: 10.1088/1681-7575/aa4e59 [30] PARTHEY C G, MATVEEV A, ALNIS J, et al. Phys Rev Lett, 2010, 104: 233001. doi: 10.1103/PhysRevLett.104.233001 [31] CARLSSON B D, EKSTRÖM A, FORSSÉN C, et al. Phys Rev X, 2016, 6: 011019. doi: 10.1103/PhysRevX.6.011019 [32] WIRINGA R B, STOKS V G J, SCHIAVILLA R. Phys Rev C, 1995, 51: 38. doi: 10.1103/PhysRevC.51.38 [33] PUDLINER B S, PANDHARIPANDE V R, CARLSON J, et al. Phys Rev Lett, 1995, 74: 4396. doi: 10.1103/PhysRevLett.74.4396 [34] ENTEM D R, MACHLEIDT R. Phys Rev C, 2003, 68: 041001. doi: 10.1103/PhysRevC.68.041001 [35] NAVRÁTIL P. Few-Body Syst, 2007, 41: 117. doi: 10.1007/s00601-007-0193-3 [36] FRANKE B, KRAUTH J J, ANTOGNINI A, et al. Eur Phys J D, 2017, 71: 341. doi: 10.1140/epjd/e2017-80296-1 [37] DIEPOLD M, FRANKE B, KRAUTH J J, et al. Ann Phys, 2018, 396: 220. doi: 10.1016/j.aop.2018.07.015 [38] ZHENG X, SUN Y R, CHEN J J, et al. Phys Rev Lett, 2017, 119: 263002. doi: 10.1103/PhysRevLett.119.263002 [39] ROSENFELDER R. Nucl Phys A, 1983, 393: 301. doi: 10.1016/0375-9474(83)90144-6 [40] LEIDEMANN W, ROSENFELDER R. Phys Rev C, 1995, 51: 427. doi: 10.1103/PhysRevC.51.427 -
点击查看大图
图(3) / 表 (3)
计量
- 文章访问数: 916
- HTML全文浏览量: 110
- PDF下载量: 36
- 被引次数: 0
甘公网安备 62010202000723号