-
The Quark-Gluon Plasma (QGP) is predicted by the Quantum Chromodynamics (QCD) as a new matter state containing deconfined quarks and gluons under extremely high temperature and density. It is believed to have been produced in the early universe after the Big Bang. Recent experimental results from the Relativistic Heavy-Ion Collider (RHIC) at Brookhaven National Laboratory (BNL) and the Large Hadron Collider (LHC) at European Organization for Nuclear Research (CERN) support that a strongly coupled QGP (sQGP) has been created in ultra-relativistic heavy-ion collisions, mimicking the early universe[1-2]. To study the properties of the QGP and its evolution is particularly helpful for understanding the early universe.
Charm and beauty are called as heavy quarks due to their much larger masses compared to those of light quarks (u, d and s). Heavy quarks are believed to be created predominantly via initial hard scatterings before the formation of the QGP in the early stage of heavy-ion collisions[3-4], and to experience the full time evolution of the QGP. Their total yields can be evaluated by the perturbative-QCD (pQCD) theory and be scaled with the number of binary collisions (
$ N_{\rm coll} $ )[4]. For these reasons, heavy quarks are always considered as ideal probes for studying the properties of the QGP.When partons travel inside the hot-dense medium and interact with the medium constituents, they deposite energy into the medium. Theoretical calculations predict that the radiative part of the partonic energy loss is mass dependent[5]. The energy loss of heavy quarks should be smaller than that of light quarks due to the suppression of the gluon radiation in the forward angle by the quark mass, and beauty would lose even less energy than charm for it is three times heavier than charm quark. The heavy quark production as a function of the transverse momentum (
$ p_{{\rm{T}}} $ ) is predicted to be modified by their energy loss[6], which, experimentally, is usually characterized by the nuclear modification factor ($ R_{{\rm{AA}}} $ )[7] defined as$$ \begin{aligned} R_{{\rm{AA}}}\left(p_{\rm T}\right) = \frac{1}{\left\langle N_{\rm coll}\right\rangle}\frac{\left. {\rm{d}} N_{\rm AA}\middle/ {\rm{d}} p_{\rm T}\right.}{\left. {\rm{d}} N_{\rm pp}\middle/ {\rm{d}} p_{\rm T}\right.}, \end{aligned} $$ (1) where
$ \left. {\rm{d}} N_{\rm AA}\middle/ {\rm{d}} p_{\rm T}\right. $ and$ \left. {\rm{d}} N_{\rm pp}\middle/ {\rm{d}} p_{\rm T}\right. $ are particle production yields in A+A and p+p collisions, respectively, and$ \left\langle N_{\rm coll}\right\rangle $ is the average$ N_{\rm coll} $ often calculated using a Monte Carlo Glauber model. The$ \left. {\rm{d}} N_{\rm pp}\middle/ {\rm{d}} p_{\rm T}\right. $ is used as the baseline since there is no QGP created in p+p collisions. With the normalization of$ \left\langle N_{\rm coll}\right\rangle $ ,$ R_{{\rm{AA}}} $ should be equal to unity if there is no medium effect in A+A collisions. Partonic energy loss could result in a suppression on the value of$ R_{{\rm{AA}}} $ at moderate-to-high$ p_{{\rm{T}}} $ . Recent measurements on the$ R_{{\rm{AA}}} $ of open charm hadrons show strong suppression at high$ p_{{\rm{T}}} $ with a similar magnitude as light flavor hadrons, suggesting significant interactions between charm and the sQGP medium[8]. However, most of heavy flavor electron (HFE) measurements report results on electrons from heavy flavor decays without charm and beauty components separated due to technique limits, and large uncertainties are reported in a few existing separations for these two components[9].An anisotropic collectivity exists in the expanding medium created in heavy-ion collisions[10]. Light quarks are unable to prevent themselves from following the collective flow and achieving thermal equilibrium[11]. However, heavy quarks are expected to be more difficult to mobilize and to obtain anisotropic momenta because of their much larger masses. To describe the azimuthal anisotropy, a Fourier expansion of the azimuthal angle (
$ \varphi $ ) is obatined in the momentum space as[12]$$ \begin{aligned} E\frac{ {\rm{d}}^{3}N}{ {\rm{d}}^{3}p} = \frac{ {\rm{d}}^{2}N}{2\pi p_{\rm T} {\rm{d}} p_{\rm T} {\rm{d}} y}\left\{1+\sum\limits_{n = 1}^{\infty}2v_{n}\cos\big[n\left(\varphi-\psi_{\rm R}\right)\big]\right\}, \end{aligned} $$ (2) where
$ \psi_{\rm R} $ denotes the reaction plane (defined by the beam axis and the direction of the impact parameter between two colliding nuclei). And the elliptic flow ($ v_{2} $ ) is defined as the 2nd cofficient$$ \begin{array}{l} v_{2}\left(p_{\rm T}\right) = \left\langle\cos\left[2\left(\varphi-\psi_{\rm R}\right)\right]\right\rangle. \end{array} $$ (3) The heavy quark
$ v_{2} $ is proposed to be a significant observable for quantifying partonic matter properties, such as the thermalization[6]. Recent measurements shows that charm gains significant flow like light quarks through interactions with the sQGP medium[13]. Because beauty is three times heavier than charm, its behavior in the anisotropic collective flow could be different from that of charm. However, most of heavy flavor$ v_{2} $ measurements are for charmed hadrons or the HFE and there are few results for beauty$ v_{2} $ via either hadronic decays or semileptonic channels at RHIC. -
We have developed a data-driven method to separate charm and beauty components from the HFE measurements on
$ p_{{\rm{T}}} $ spectra and on$ R_{{\rm{AA}}} $ and$ v_{2} $ distributions based on the most recent charmed hadron measurements at mid-rapidity in minimum bias (Min bias) Au+Au collisions at$ \sqrt{s_{{\rm{NN}}}} $ = 200 GeV at RHIC. Parts of heavy flavor hadrons decay to light flavor hadrons and leptons, such as electrons, via semileptonic channels. These electrons carry information about the properties of origin heavy quarks.It is started from the charmed hadron measurements on
$ p_{{\rm{T}}} $ spectra of$ {\rm{D}}^{0} $ [8],$ {\rm{D}}^{\pm} $ [14],$ {\rm{D}}_{\rm s} $ [14],$ {{\Lambda}}_{\rm c} $ [15] and$ {{\rm{J}}/\psi } $ [16-17] at mid-rapidity in Au+Au collisions at$ \sqrt{s_{{\rm{NN}}}} $ =200 GeV with the STAR experiment at RHIC, all of which are parameterized and shown with uncertainty bands in Fig. 1. Measurements on$ {\rm{D}}^{0} $ at 0~80%,$ {\rm{D}}_{\rm s} $ at 10%~40% and$ {{\rm{J}}/\psi } $ at 0~60% are used because of their largest statistics and best precision, and they are parameterized and extrapolated to 0$ < $ $ p_{{\rm{T}}} $ $ < $ 20 GeV/$ c $ with the Levy function[18]
Figure 1. (color online) Measured and parameterized
$p_{{\rm{T}}}$ spectra with uncertainty bands of charmed hadrons (${\rm{D}}^{0}$ [8],${\rm{D}}^{\pm}$ [14],${\rm{D}}_{\rm s}$ [14],${{\Lambda}}_{\rm c} $ [15],${{\rm{J}}/\psi }$ [16-17]) at mid-rapidity in Au+Au collisions at$\sqrt{s_{{\rm{NN}}}}$ = 200 GeV.$$ \begin{split} \frac{ {\rm{d}}^{2}N}{2\pi p_{\rm T} {\rm{d}} p_{\rm T} {\rm{d}} y} = & \frac{1}{2\pi}\frac{ {\rm{d}} N}{ {\rm{d}} y}\frac{(n-1)(n-2)}{nT[nT+m_{0}(n-2)]}\times\\ &\left(1+\frac{\sqrt{p_{\rm T}^{2}+m_{0}^{2}}-m_{0}}{nT}\right)^{-n}, \end{split} $$ (4) and the power-law function[19]
$$ \begin{split} \frac{ {\rm{d}}^{2}N}{2\pi p_{\rm T} {\rm{d}} p_{\rm T} {\rm{d}} y} =& \frac{2}{\pi}\frac{ {\rm{d}} N}{ {\rm{d}} y}\frac{(n-1)(n-2)}{(n-3)^{2}\left\langle p_{\rm T}\right\rangle^{2}}\times\\ &\left(1+\frac{2p_{\rm T}}{\left\langle p_{\rm T}\right\rangle(n-3)}\right)^{-n}, \end{split} $$ (5) where
$ m_{0} $ is the rest mass of the particle. Halves of the differences between Levy and power-law fits are quadratically summed into uncertainty bands. The$ {\rm{D}}^{\pm} $ spectrum is obtained by scaling the$ {\rm{D}}^{0} $ spectrum with a constant (0.429$ \!\pm \! $ 0.038) fitted from the$ \rm D^\pm/D^0 $ ratio measured at 0~10% centrality, since there is no obverse$ p_{{\rm{T}}} $ dependence observed. Because$ {\rm{D}}^{0} $ and$ {\rm{D}}^{\pm} $ make up the triplet state of D-mesons, their properties, including shapes of the$ p_{{\rm{T}}} $ spectra, should be highly consistent. The$ {{\Lambda}}_{\rm c} $ spectrum is fitted and extrapolated to the$ p_{{\rm{T}}} $ range of 0~10 GeV/$ c $ with the measured$ {\rm{D}}^{0} $ spectrum multiplied by the average of different model calculations on$ {\Lambda}_{\rm c}/{\rm{D}}^0 $ ratio: Ko[20], Greco[21] and Tshingua[22] with their differences as the uncertainty.All aforementioned parameterized
$ p_{{\rm{T}}} $ spectra of charmed hadrons are input into Monte Carlo simulations of semileptonic decays to electrons, of which the$ {\rm{J}/\psi }$ spectrum is input in a Pythia decayer[23] decaying to$ {\rm e}^{+}{\rm e}^{-} $ . In each simulated event, we sample the hadron$ p_{{\rm{T}}} $ from a uniform distribution with$ \frac{ {\rm{d}} N}{ {\rm{d}} p_{\rm T}} $ in this$ p_{{\rm{T}}} $ bin as the weight in order to increase the statistics at higher$ p_{{\rm{T}}} $ . The 4-momentum is determined additionally with a uniformly distributed azimuthal angle$ \varphi $ , a gaussian mid-rapidity$ y $ and the hadron mass. And the electron momentum in the hadron rest frame is sampled from the measured distribution[24]. After Lorentz transformation, the final electron$ p_{{\rm{T}}} $ from semileptonic decays in the laboratory frame can be obtained. The output electrons are filled in the$ \frac{ {\rm{d}} N}{2\pi p_{\rm T} {\rm{d}} p_{\rm T}} $ distribution. Upper and lower hadron spectrum uncertainties are also input into the simulations and propagated to the output accordingly.The output electron
$ p_{{\rm{T}}} $ spectra are normalized by measured cross sections of parent hadrons and semileptonic decay branching ratios. In particular, those from$ {\rm{D}}_{\rm s} $ ,$ {{\Lambda}}_{\rm c} $ and$ {{\rm{J}}/\psi }$ are scaled by$ N_{\rm coll} $ to 0~80% centrality from 10%~40%, 10%~80% and 0~60%, respectively. Uncertainties of branching ratios,$ N_{\rm coll} $ normalization (for$ {\rm{D}}_{\rm s} $ ,$ {{\Lambda}}_{\rm c} $ and$ {{\rm{J}}/\psi }$ ) and the$ {\rm D}^{\pm}/{\rm D}^0 $ ratio (for$ {\rm{D}}^{\pm} $ ) are also taken into account and propagated quadratically. Fig. 2 shows the final electron$ p_{{\rm{T}}} $ spectra from charmed hadron decays and the summed charm component ($ {\rm{c\rightarrow e}} $ ) with shaded bands as uncertainties at mid-rapidity in minimum bias Au+Au collisions at$ \sqrt{s_{{\rm{NN}}}} $ =200 GeV. The electron spectrum from beauty decays ($ {\rm{b\rightarrow e}} $ ) is calculated by subtracting the$ {\rm{c\rightarrow e}} $ component from the HFE spectrum measured by STAR[25]. The$ {\rm{c\rightarrow e}} $ uncertainty contributions to the last two points of$ {\rm{b\rightarrow e}} $ at$ p_{{\rm{T}}} $ $ > 7$ GeV/$ c $ are safely doubled due to higher$ p_{{\rm{T}}} $ extrapolation of charmed hadron spectra.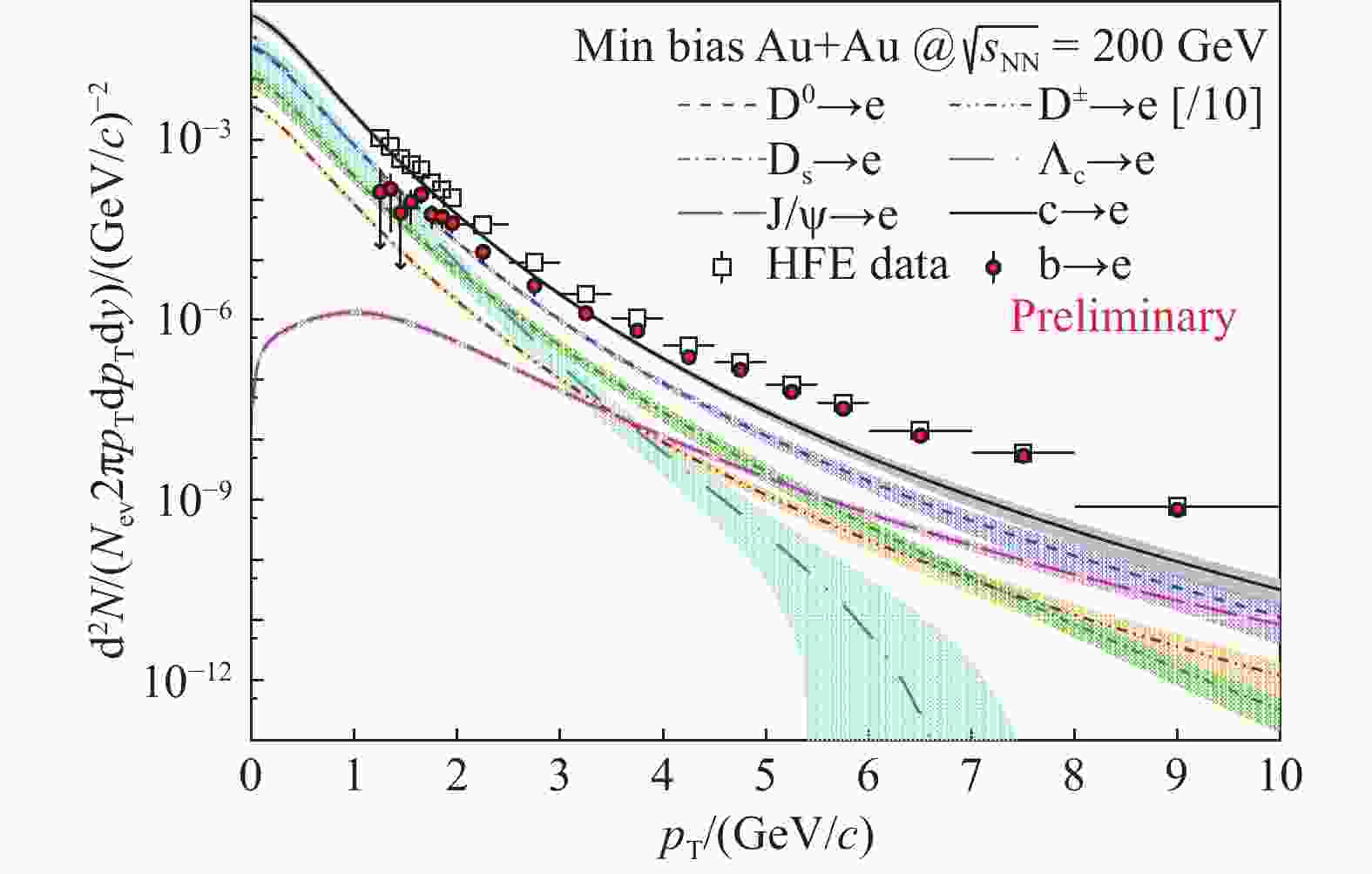
Figure 2. (color online) Electron
$p_{{\rm{T}}}$ spectra from charmed hadron decays and the sum of them (${\rm{c\rightarrow e}}$ ) with uncertainty bands at mid-rapidity in minimum bias Au+Au collisions at$\sqrt{s_{{\rm{NN}}}}$ =200 GeV. The electron spectrum from beauty decays (${\rm{b\rightarrow e}}$ ) is obtained by subtracting${\rm{c\rightarrow e}}$ from the HFE data.The beauty component fraction in the HFE spectrum is defined as
$$ \begin{aligned} f^{ {\rm{b\rightarrow e}}} = \frac{\left. {\rm{d}} N^{ {\rm{b\rightarrow e}}}\middle/ {\rm{d}} p_{\rm T}\right.}{\left. {\rm{d}} N^{\rm HFE}\middle/ {\rm{d}} p_{\rm T}\right.}. \end{aligned} $$ (6) Fig. 3 shows the
$ f^{ {\rm{b\rightarrow e}}} $ at mid-rapidity in minimum bias Au+Au collisions at$ \sqrt{s_{{\rm{NN}}}} $ =200 GeV ($ f_{{\rm{AA}}}^{ {\rm{b\rightarrow e}}} $ ) obtained from Fig. 2 compared with previous measurements in p+p collisions ($ f_{{\rm{pp}}}^{ {\rm{b\rightarrow e}}} $ ) by STAR[26] (red open squares) and by PHENIX[27] (green crosses). The fixed-order next-to-leading log (FONLL) calculation[4] is presented as the gray dashed curve, with which the STAR p+p data are parameterized (cyan dashed curve with band). Blue solid squares denote the average of the STAR and the PHENIX p+p data with half of their difference taken into account in the uncertainty bars. At$ p_{{\rm{T}}} \sim $ 3.5 GeV/$ c $ , beauty and charm components are comparable. The$ f_{{\rm{AA}}}^{ {\rm{b\rightarrow e}}} $ looks systematically higher than$ f_{{\rm{pp}}}^{ {\rm{b\rightarrow e}}} $ , in particular in$ p_{{\rm{T}}} > 7$ GeV/$ c $ where$ f_{{\rm{AA}}}^{ {\rm{b\rightarrow e}}} $ increases up to (90$ \pm $ 10)%.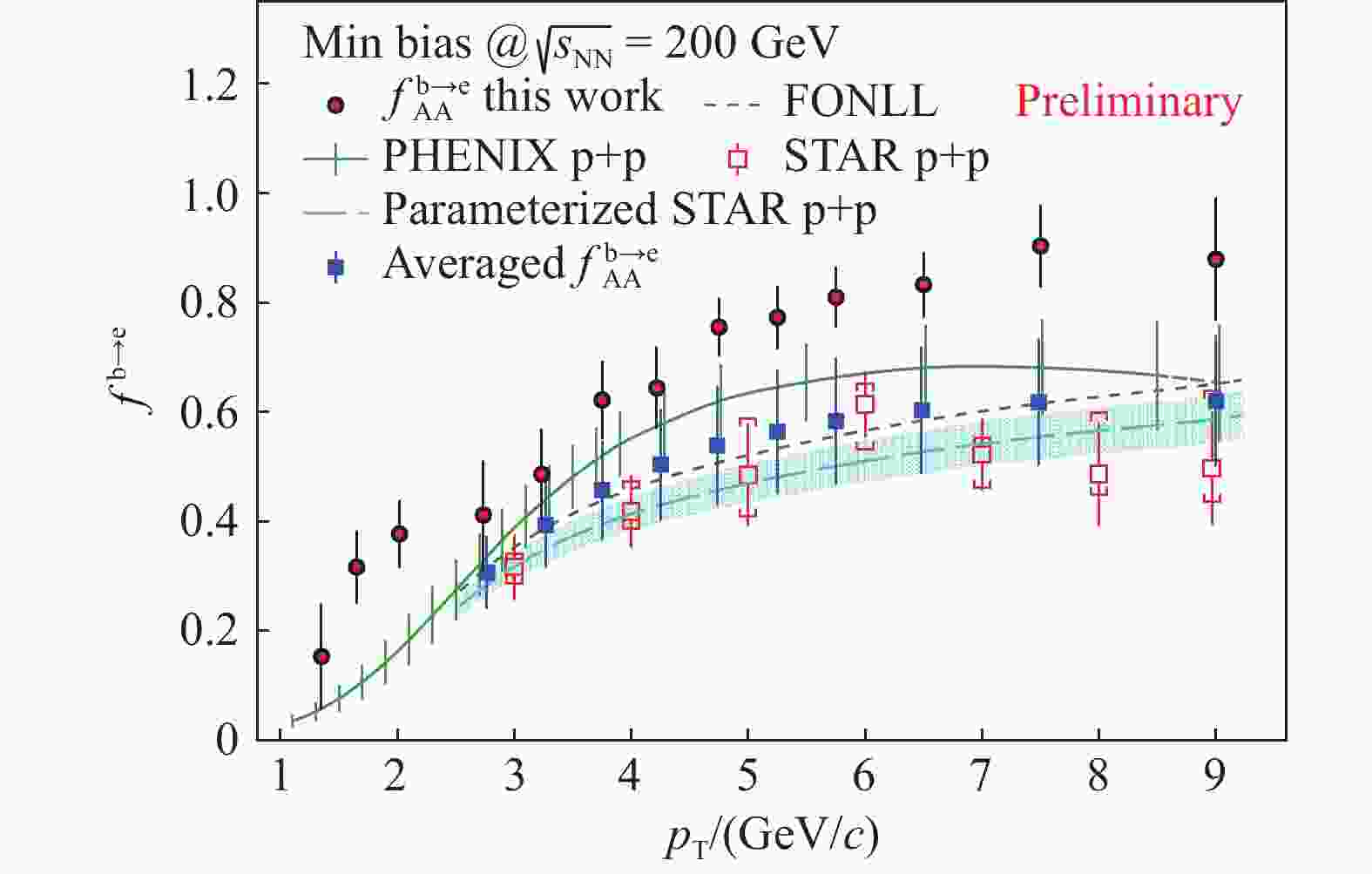
Figure 3. (color online) Fractions of beauty decay electrons in the HFE (
$f^{ {\rm{b\rightarrow e}}}$ ) at mid-rapidity in minimum bias Au+Au collisions at$\sqrt{s_{{\rm{NN}}}}$ =200 GeV compared with the FONLL theoretical calculation[4] and measurements by STAR[26], by PHENIX[27] and their average in p+p collisions. The last point of the PHENIX p+p data at 9 GeV/c is extrapolated. -
The
$ R_{{\rm{AA}}} $ of electrons from charm and from beauty decays ($ R_{{\rm{AA}}}^{ {\rm{c\rightarrow e}}} $ and$ R_{{\rm{AA}}}^{ {\rm{b\rightarrow e}}} $ ) as functions of$ p_{{\rm{T}}} $ can be extracted from the$ R_{{\rm{AA}}} $ of the HFE ($ R_{{\rm{AA}}}^{\rm HFE} $ ) measured by STAR[25] with$$ \begin{aligned} R_{{\rm{AA}}}^{ {\rm{c\rightarrow e}}} = \dfrac{1- f_{{\rm{AA}}}^{ {\rm{b\rightarrow e}}}}{1- f_{{\rm{pp}}}^{ {\rm{b\rightarrow e}}}} R_{{\rm{AA}}}^{\rm HFE}, \end{aligned} $$ (7) $$ \begin{aligned} R_{{\rm{AA}}}^{ {\rm{b\rightarrow e}}} = \dfrac{ f_{{\rm{AA}}}^{ {\rm{b\rightarrow e}}}}{ f_{{\rm{pp}}}^{ {\rm{b\rightarrow e}}}} R_{{\rm{AA}}}^{\rm HFE}, \end{aligned} $$ (8) which are shown as blue solid squares and red solid circles in Fig. 4, respectively. The
$ f_{{\rm{pp}}}^{ {\rm{b\rightarrow e}}} $ here denotes the averaged one of STAR and PHENIX p+p data in Fig. 3. As a cross-check, two red dashed curves representing$ \rm b(c)\rightarrow e/FONLL $ are obtained directly by the definition of$ R_{{\rm{AA}}} $ in Eq. (1) and show a good agreement with our results. Results of this work are consistent with the HFT template analysis (open green symbols)[9] and show improved precision. The$ R_{{\rm{AA}}}^{ {\rm{b\rightarrow e}}} $ result is consistent with the DUKE model prediction[28], but$ R_{{\rm{AA}}}^{ {\rm{c\rightarrow e}}} $ is clearly lower than the prediction in$ p_{{\rm{T}}} > 4 $ GeV/$ c $ . Less suppression of$ R_{{\rm{AA}}}^{ {\rm{b\rightarrow e}}} $ compared with that of$ R_{{\rm{AA}}}^{ {\rm{c\rightarrow e}}} $ can be observed, which could indicate the possible mass dependence of the energy loss of charm and beauty.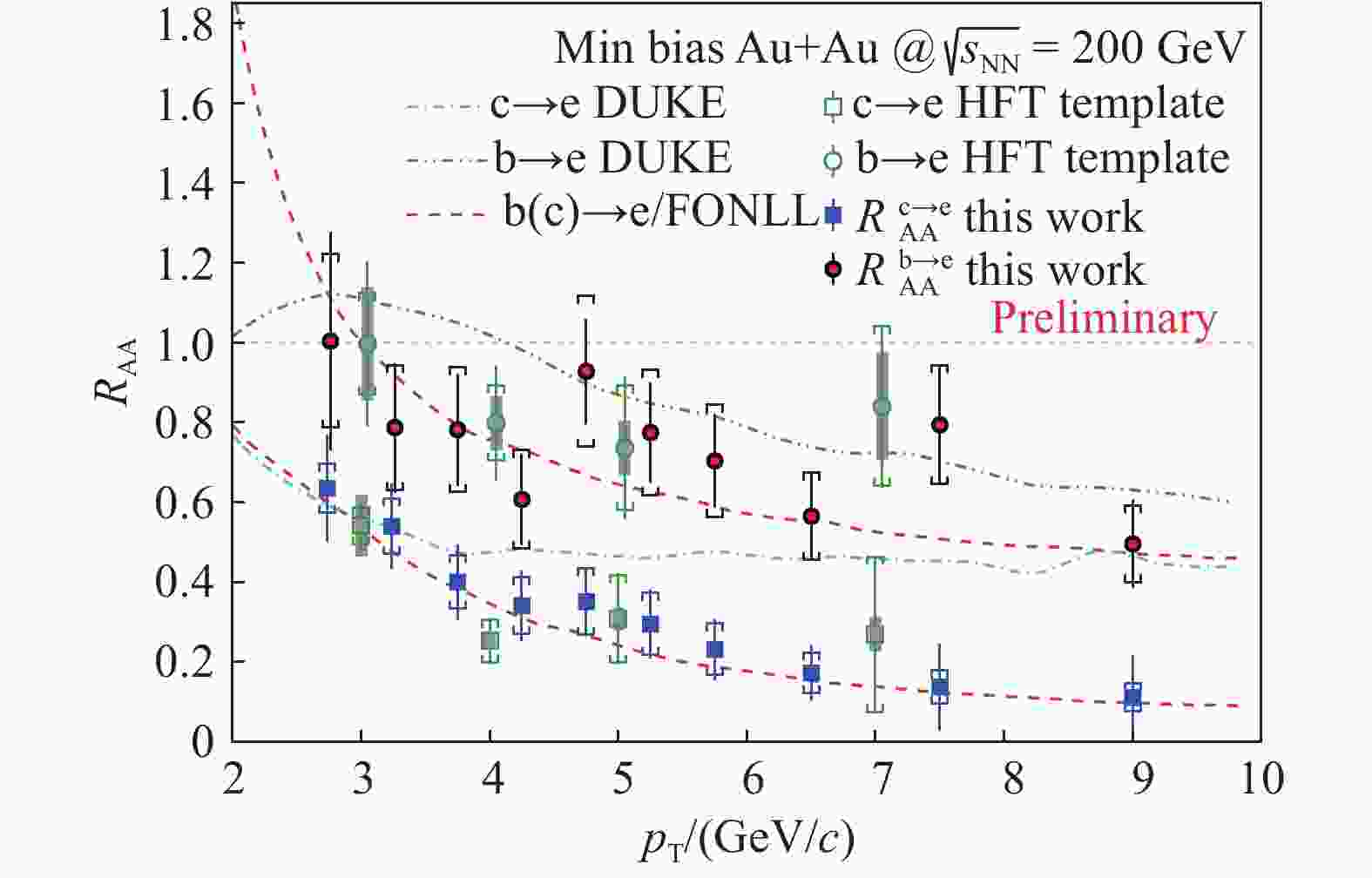
Figure 4. (color online) The nuclear modification factors (
$R_{{\rm{AA}}}$ ) of${\rm{c\rightarrow e}}$ and${\rm{b\rightarrow e}}$ with HFT template analysis[9] and DUKE model predictions[28] as comparisons at mid-rapidity in minimum bias Au+Au collisions at$\sqrt{s_{{\rm{NN}}}}$ =200 GeV. Uncertainty bars of this work denote quadratically summed contributions of$f_{{\rm{AA}}}^{\rm b(c)\rightarrow e}$ and$R_{{\rm{AA}}}^{\rm HFE}$ and boxes are from$f_{{\rm{pp}}}^{ {\rm{b\rightarrow e}}}$ .$\rm b(c)\rightarrow e/FONLL$ are obtained directly with the$R_{{\rm{AA}}}$ definition. -
The
$ {\rm{D}}^{0} $ $ v_2 $ at 0~80% centrality measured by STAR[13] is parameterized by Eq. (9)[29] with the linear term forced to pass through the origin according to the properties of$ v_2 $ ,$$ \begin{split} v_2\left(p_{\rm T}\right) = \dfrac{p_0 n}{1+{\rm exp}\left(\dfrac{p_1-\frac{p_{\rm T}}{n}}{p_2}\right)}-\dfrac{p_0 n}{1+{\rm exp}\left(\dfrac{p_1}{p_2}\right)}-p_3 np_{\rm T}, \end{split} $$ (9) where
$ n $ is the number of constituent quarks,$ p_i $ ($ i $ = 0, 1, 2, 3) are free parameters. The$ v_2 $ distributions of D-mesons ($ n_{\rm quarks} $ = 2) and$ {{\Lambda}}_{\rm c} $ ($ n_{\rm quarks} $ = 3) are obtained with the number-of-constituent-quark (NCQ) scaling assumption[29-30] as$ \left.v_{2}\big/n\right. $ vs.$ \left.\left(\sqrt{p_{\rm T}^{2}\!+\!m_{0}^{2}}\!-\!m_{0}\right)\!\big/\!n\right. $ from the parameterized$ {\rm{D}}^{0} $ $ v_2 $ . Semileptonic decays of charmed hadrons are simulated with the hadron$ p_{{\rm{T}}} $ spectra and$ v_{2} $ distributions as inputs. Different from the simulations in Sec. 2, the azimuthal angle$ \varphi $ in each$ p_{{\rm{T}}} $ bin is sampled from the distribution[29]$$ \begin{aligned} \dfrac{{\rm d}N}{{\rm d}\varphi} = 1+2v_{2}{\rm cos}(2\varphi). \end{aligned} $$ (10) The
$ v_2 $ of$ \rm D\rightarrow e $ ($ v_{2}^{\rm D\rightarrow e} $ ) and$\Lambda_{\rm c}\rightarrow {\rm e}$ ($v_{2}^{\Lambda_{\rm c}\rightarrow {\rm e}}$ ) as functions of$ p_{{\rm{T}}} $ can be obtained by fitting the output electron$ \varphi $ distributions with Eq. (10) in different$ p_{{\rm{T}}} $ bins. The uncertainty bands of charmed hadron$ v_2 $ from parameterization are also input into the simulations and propagated to electron$ v_2 $ distributions.The
$ v_2 $ of$ {\rm{c\rightarrow e}} $ ($ v_{2}^{ {\rm{c\rightarrow e}}} $ ) is an average of$ v_{2}^{\rm D\rightarrow e} $ and$v_{2}^{\Lambda_{\rm c}\rightarrow {\rm e}}$ with their relative production yields in Fig. 2 as weights. In a similar way, the$ v_2 $ of$ {\rm{b\rightarrow e}} $ ($ v_{2}^{ {\rm{b\rightarrow e}}} $ ) can be extracted with$$ \begin{split} v_{2}^{ {\rm{b\rightarrow e}}} = \dfrac{v_{2}^{\rm HFE}-\left(1- f_{{\rm{AA}}}^{ {\rm{b\rightarrow e}}}\right)v_{2}^{ {\rm{c\rightarrow e}}}}{ f_{{\rm{AA}}}^{ {\rm{b\rightarrow e}}}}, \end{split} $$ (11) where
$ v_{2}^{\rm HFE} $ denotes the$ v_2 $ of the HFE obtained by parameterizing the combined distribution measured by STAR[25] and PHENIX[31] with Eq. (9). Fig. 5 shows the results of$ v_{2}^{ {\rm{c\rightarrow e}}} $ (blue solid squares) and$ v_{2}^{ {\rm{b\rightarrow e}}} $ (red solid circles). As a comparison, the$ v_2 $ of$ \rm \phi\rightarrow e $ ($ v_{2}^{\rm \phi\rightarrow e} $ ) shown as red open squares is calculated in the same way with the$ \rm \phi $ -meson$ p_{{\rm{T}}} $ spectrum[32] and$ v_2 $ [33] at 0~80% centrality as inputs of the Pythia decayer. A non-zero$ v_{2}^{ {\rm{b\rightarrow e}}} $ in$ p_{{\rm{T}}} > $ 3.0 GeV/$ c $ is observed and consistent with the electron$ v_2 $ from charmed and strange hadron decays within uncertainties in$ p_{{\rm{T}}} > $ 4.5 GeV/$ c $ . However,$ v_{2}^{ {\rm{b\rightarrow e}}} $ is clearly smaller than$ v_{2}^{ {\rm{c\rightarrow e}}} $ at 1.5 GeV/$ c < $ $ p_{{\rm{T}}} < $ 4.0 GeV/$ c $ . In addition, we unfold the B-meson$ p_{{\rm{T}}} $ spectrum from the$ {\rm{b\rightarrow e}} $ points extracted in Fig. 2 and assume that the B-meson$ v_2 $ follows the NCQ scaling. The black dashed curve represents the refolded$ v_{2}^{\rm b\rightarrow e} $ with the Pythia decayer and our$ v_{2}^{ {\rm{b\rightarrow e}}} $ result deviates from it at 2.5 GeV/$ c < $ $ p_{{\rm{T}}} < $ 4.5 GeV/$ c $ with a confidence level of 98.2% ($ \chi^2/ndf $ = 11.92/4), which could be related to the beauty thermalization or its hadronization mechanism in the QGP.
Figure 5. (color online) The elliptic flows (
$v_2$ ) of${\rm{c\rightarrow e}}$ and${\rm{b\rightarrow e}}$ at mid-rapidity in minimum bias Au+Au collisions at$\sqrt{s_{{\rm{NN}}}}$ =200 GeV. The uncertainty of$v_{2}^{ {\rm{b\rightarrow e}}}$ is propagated from$v_{2}^{\rm HFE}$ (bars),$v_{2}^{ {\rm{c\rightarrow e}}}$ (brackets) and$f_{{\rm{AA}}}^{ {\rm{b\rightarrow e}}}$ (grey bands). The$v_{2}^{\rm b\rightarrow e}$ with the NCQ scaling assumption of the B-meson$v_2$ and$v_{2}^{\rm \phi\rightarrow e}$ are shown as comparisons. -
This paper reports a data-driven method developed to separate charm and beauty components from heavy flavor electron measurements at mid-rapidity in minimum bias Au+Au collisions at RHIC. Semileptonic decays of charmed hadrons are simulated with the most recent measurements on charmed hadrons with RHIC-STAR as inputs. By subtracting the output electrons from charm decays, the beauty component is extracted from the HFE spectrum, and the
$ p_{{\rm{T}}} $ spectra,$ R_{{\rm{AA}}} $ and$ v_2 $ distributions of electrons from charm and from beauty decays are obtained. In these preliminary results, less suppression of$ R_{{\rm{AA}}}^{ {\rm{b\rightarrow e}}} $ is observed than that of$ R_{{\rm{AA}}}^{ {\rm{c\rightarrow e}}} $ at moderate-to-high$ p_{{\rm{T}}} $ , and$ v_{2}^{ {\rm{b\rightarrow e}}} $ is smaller than$ v_{2}^{ {\rm{c\rightarrow e}}} $ ,$ v_{2}^{\rm \phi\rightarrow e} $ and the$ v_{2}^{ {\rm{b\rightarrow e}}} $ with the B-meson$ v_2 $ NCQ scaling assumption at low-to-moderate$ p_{{\rm{T}}} $ . Improved results further elucidating charm and beauty physics in heavy-ion collisions will be available in the near future.
-
摘要: 重味夸克(即粲和底),尤其是底夸克,具有预期不同于轻夸克的性质,被认为是夸克胶子等离子体的理想探针。然而,很少有对底强子或其衰变的轻子的测量。利用最近相对论重离子对撞机上
$\sqrt{s_{\rm NN}}=200\;{\rm{GeV}}$ 的金核-金核碰撞中产生于中心快度下的粲强子和重味衰变电子的测量数据,我们发展了一种数据驱动的方法,用于分离重味衰变电子中粲和底的成分。从粲强子的测量数据出发,通过模拟其半轻子衰变得到粲衰变电子,从而从重味衰变电子中提取出底的成分。初步的结果展示了在最小偏向的金核-金核碰撞中粲和底衰变电子的横动量谱、核修正因子和椭圆流的分布。在中等至较高横动量区,相比于粲衰变电子的核修正因子,底衰变电子的核修正因子受到了较小的压制;在较低至中等横动量区,底衰变电子获得了比粲衰变电子更小的椭圆流。-
关键词:
- charm /
- beauty /
- electron /
- transverse momentum /
- nuclear modification factor /
- elliptic flow
Abstract: Heavy quarks (charm and beauty), especially beauty, with expectedly different properties from light quarks are considered as ideal probes for the Quark-Gluon Plasma (QGP). However, there are few measurements on beauty hadrons or on their decay leptons. With the most recent measurements on charmed hadrons and heavy flavor decay electrons (HFE) at mid-rapidity in Au+Au collisions at$\sqrt{s_{\rm NN}}=200\;{\rm{GeV}}$ at RHIC, a data-driven method is developed to separate charm and beauty components from the HFE measurements. From charmed hadron measurements, electrons from charm decays via semileptonic decay simulations are obtained, with which the beauty component can be extracted from the HFE spectrum. As preliminary results, the$p^{}_{\rm T}$ spectra,$R_{\rm AA}$ and$v_2$ distributions of electrons from charm and from beauty decays ($R_{\rm AA}^{\rm c\rightarrow e}$ and$v_2^{\rm c\rightarrow e}$ ,$R_{\rm AA}^{\rm b\rightarrow e}$ and$v_2^{\rm b\rightarrow e}$ ) in minimum bias Au+Au collisions are presented, respectively. Less suppression of$R_{\rm AA}^{\rm b\rightarrow e}$ is observed compared with that of$R_{\rm AA}^{\rm c\rightarrow e}$ at moderate-to-high$p_{\rm T}$ , and$v_2^{\rm b\rightarrow e}$ shows smaller than$v_2^{\rm c\rightarrow e}$ at low-to-moderate$p_{\rm T}$ .-
Key words:
- charm /
- beauty /
- electron /
- transverse momentum /
- nuclear modification factor /
- elliptic flow
-
Figure 1. (color online) Measured and parameterized
$p_{{\rm{T}}}$ spectra with uncertainty bands of charmed hadrons (${\rm{D}}^{0}$ [8],${\rm{D}}^{\pm}$ [14],${\rm{D}}_{\rm s}$ [14],${{\Lambda}}_{\rm c} $ [15],${{\rm{J}}/\psi }$ [16-17]) at mid-rapidity in Au+Au collisions at$\sqrt{s_{{\rm{NN}}}}$ = 200 GeV.Figure 2. (color online) Electron
$p_{{\rm{T}}}$ spectra from charmed hadron decays and the sum of them (${\rm{c\rightarrow e}}$ ) with uncertainty bands at mid-rapidity in minimum bias Au+Au collisions at$\sqrt{s_{{\rm{NN}}}}$ =200 GeV. The electron spectrum from beauty decays (${\rm{b\rightarrow e}}$ ) is obtained by subtracting${\rm{c\rightarrow e}}$ from the HFE data.Figure 3. (color online) Fractions of beauty decay electrons in the HFE (
$f^{ {\rm{b\rightarrow e}}}$ ) at mid-rapidity in minimum bias Au+Au collisions at$\sqrt{s_{{\rm{NN}}}}$ =200 GeV compared with the FONLL theoretical calculation[4] and measurements by STAR[26], by PHENIX[27] and their average in p+p collisions. The last point of the PHENIX p+p data at 9 GeV/c is extrapolated.Figure 4. (color online) The nuclear modification factors (
$R_{{\rm{AA}}}$ ) of${\rm{c\rightarrow e}}$ and${\rm{b\rightarrow e}}$ with HFT template analysis[9] and DUKE model predictions[28] as comparisons at mid-rapidity in minimum bias Au+Au collisions at$\sqrt{s_{{\rm{NN}}}}$ =200 GeV. Uncertainty bars of this work denote quadratically summed contributions of$f_{{\rm{AA}}}^{\rm b(c)\rightarrow e}$ and$R_{{\rm{AA}}}^{\rm HFE}$ and boxes are from$f_{{\rm{pp}}}^{ {\rm{b\rightarrow e}}}$ .$\rm b(c)\rightarrow e/FONLL$ are obtained directly with the$R_{{\rm{AA}}}$ definition.Figure 5. (color online) The elliptic flows (
$v_2$ ) of${\rm{c\rightarrow e}}$ and${\rm{b\rightarrow e}}$ at mid-rapidity in minimum bias Au+Au collisions at$\sqrt{s_{{\rm{NN}}}}$ =200 GeV. The uncertainty of$v_{2}^{ {\rm{b\rightarrow e}}}$ is propagated from$v_{2}^{\rm HFE}$ (bars),$v_{2}^{ {\rm{c\rightarrow e}}}$ (brackets) and$f_{{\rm{AA}}}^{ {\rm{b\rightarrow e}}}$ (grey bands). The$v_{2}^{\rm b\rightarrow e}$ with the NCQ scaling assumption of the B-meson$v_2$ and$v_{2}^{\rm \phi\rightarrow e}$ are shown as comparisons. -
[1] ADAMS J, AGGARWAL M M, AHAMMED Z, et al. Nucl Phys A, 2005, 757(1-2): 102. doi: 10.1016/j.nuclphysa.2005.03.085 [2] MULLER B, SCHUKRAFT J, WYSLOUCH B. Ann Rev Nucl Part Sci, 2012, 62(1): 361. doi: 10.1146/annurev-nucl-102711-094910 [3] LIN Z, GYULASSY M. Phys Rev C, 1995, 51(4): 2177. doi: 10.1103/PhysRevC.51.2177 [4] CACCIARI M, NASON P, VOGT R. Phys Rev Lett, 2005, 95(12): 2001. doi: 10.1103/PhysRevLett.95.122001 [5] BUZZATTI A, GYULASSY M. Phys Rev Lett, 2012, 108: 2301. doi: 10.1103/PhysRevLett.108.022301 [6] MOORE D G, TEANEY D. Phys Rev C, 2005, 71(6): 4904. doi: 10.1103/PhysRevC.71.064904 [7] WANG X, GYULASSY M. Phys Rev Lett, 1992, 68(10): 1480. doi: 10.1103/PhysRevLett.68.1480 [8] ADAM J, ADAMCZYK L, ADAMS J, et al. Phys Rev C, 2019, 99(3): 4908. doi: 10.1103/PhysRevC.99.034908 [9] OH K. Nucl Phys A, 2017, 967(1): 632. doi: 10.1016/j.nuclphysa.2017.06.025 [10] ADAMS J, AGGARWAL M M, AHAMMED Z, et al. Phys Rev C, 2005, 72(1): 4904. doi: 10.1103/PhysRevC.72.014904 [11] ABELEV I B, AGGARWAL M M, AHAMMED Z, et al. Phys Rev C, 2008, 77(5): 4901. doi: 10.1103/PhysRevC.77.054901 [12] POSKANZER M A, VOLOSHIN A S. Phys Rev C, 1998, 58(3): 1671. doi: 10.1103/PhysRevC.58.1671 [13] ADAMCZYK L, ADKINS K J, AGAKISHIEV G, et al. Phys Rev Lett, 2017, 118(21): 2301. doi: 10.1103/PhysRevLett.118.212301 [14] ZHOU L. Nucl Phys A, 2017, 967(1): 620. doi: 10.1016/j.nuclphysa.2017.05.114 [15] RADHAKRISHNAN S. Nucl Phys A, 2019, 982(1): 659. doi: 10.1016/j.nuclphysa.2018.10.050 [16] ADAMCZYK L, ADKINS K J, AGAKISHIEV G, et al. Phys Rev C, 2014, 90(2): 4906. doi: 10.1103/PhysRevC.90.024906 [17] ADAMCZYK L, AGAKISHIEV G, AGGARWAL M M, et al. Phys Lett B, 2013, 722(1-3): 55. doi: 10.1016/j.physletb.2013.04.010 [18] WILK G, WLODARCZYK Z. Phys Rev Lett, 2000, 84(13): 2770. doi: 10.1103/PhysRevLett.84.2770 [19] ADAMCZYK L, AGAKISHIEV G, AGGARWAL M M, et al. Phys Rev D, 2012, 86(7): 2013. doi: 10.1103/PhysRevD.86.072013 [20] LEE H S, OHNISHI K, YASUI S, et al. Phys Rev Lett, 2008, 100(22): 2301. doi: 10.1103/PhysRevLett.100.222301 [21] GHOSH S, DAS K S, GRECO V, et al. Phys Rev D, 2014, 90(5): 4018. doi: 10.1103/PhysRevD.90.054018 [22] ZHAO J, SHI S, XU N, et al. arXiv: hep-ph/1805.10858. [23] SJÖSTRAND T, MRENNA S, SKANDS P. J High Energy Phys, 2006, 2006(5): 026. doi: 10.1088/1126-6708/2006/05/026 [24] LIU H, ZHANG Y, ZHONG C, et al. Phys Lett B, 2006, 639(5): 441. doi: 10.1016/j.physletb.2006.07.008 [25] MUSTAFA M. Nucl Phys A, 2013, 904-905(1): 665c. doi: 10.1016/j.nuclphysa.2013.02.103 [26] AGGARWAL M M, AHAMMED Z, ALAKHVERDYANTS V A, et al. Phys Rev Lett, 2010, 105(20): 2301. doi: 10.1103/PhysRevLett.105.202301 [27] AIDALA C, AKIBA Y, ALFRED M, et al. Phys Rev D, 2019, 99(9): 2003. doi: 10.1103/PhysRevD.99.092003 [28] CAO S, QIN G, BASS A S. Phys Rev C, 2015, 92(2): 4907. doi: 10.1103/PhysRevC.92.024907 [29] DONG X, ESUMI S, SORENSEN P, et al. Phys Lett B, 2004, 597(3-4): 328. doi: 10.1016/j.physletb.2004.06.110 [30] TIAN J, CHEN J, MA Y, et al. Phys Rev C, 2009, 79(6): 7901. doi: 10.1103/PhysRevC.79.067901 [31] HACHIYA T. Nucl Phys A, 2019, 982(1): 663. doi: 10.1016/j.nuclphysa.2018.10.054 [32] ABELEV I B, AGGARWAL M M, AHAMMED Z, et al. Phys Rev Lett, 2007, 99(11): 2301. doi: 10.1103/PhysRevLett.99.112301 [33] ADAMCZYK L, ADKINS K J, AGAKISHIEV G, et al. Phys Rev Lett, 2016, 116(6): 2301. doi: 10.1103/PhysRevLett.116.062301 -






















 下载:
下载:








































































































































































































































 甘公网安备 62010202000723号
甘公网安备 62010202000723号